ナッシュの定理
問題としている戦略的状況が完備情報の静学ゲームであるとともに、それが戦略型ゲーム\begin{equation*}
G=\left( I,\left\{ S_{i}\right\} _{i\in I},\left\{ u_{i}\right\} _{i\in
I}\right)
\end{equation*}として記述されているものとします。ただし、\(I\)はプレイヤー集合、\(S_{i}\)はプレイヤー\(i\in I\)の純粋戦略集合、\(u_{i}:S_{I}\rightarrow \mathbb{R} \)はプレイヤー\(i\)の利得関数です。
戦略型ゲーム\(G\)におけるプレイヤー\(i\)の混合戦略とは、自身の純粋戦略集合の要素であるそれぞれの純粋戦略\(s_{ij}\in S_{i}\)に対して、それを選択する確率\(\sigma _{i}\left( s_{ij}\right) \in \mathbb{R} \)を指定する確率測度\begin{equation*}\sigma _{i}:S_{i}\rightarrow \mathbb{R} \end{equation*}として定義されます。また、戦略型ゲーム\(G\)においてプレイヤーたちが混合戦略を採用する場合に直面する状況は\(G\)の混合拡張\begin{equation*}G^{\ast }=(I,\{\Delta \left( S_{i}\right) \}_{i\in I},\{F_{i}\}_{i\in I})
\end{equation*}として記述されます。ただし、\(I\)はプレイヤー集合、\(\Delta \left( S_{i}\right) \)はプレイヤー\(i\in I\)の混合戦略集合、\(F_{i}:\Delta \left( S_{I}\right)\rightarrow \mathbb{R} \)はプレイヤー\(i\)の期待利得関数です。
プレイヤー\(i\in I\)の混合戦略\(\sigma _{i}^{\ast }\in \Delta \left( S_{i}\right) \)が他のプレイヤーたちの混合戦略の組\(\sigma _{-i}\in\Delta \left( S_{-i}\right) \)に対する広義の最適反応であることとは、戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)において、\begin{equation*}\forall \sigma _{i}\in \Delta \left( S_{i}\right) :F_{i}(\sigma _{i}^{\ast
},\sigma _{-i})\geq F_{i}(\sigma _{i},\sigma _{-i})
\end{equation*}が成り立つことを意味します。また、プレイヤーたちの混合戦略の組\(\sigma _{I}^{\ast }=\left( \sigma_{i}^{\ast }\right) _{i\in I}\)が広義の混合戦略ナッシュ均衡であることとは、それぞれのプレイヤー\(i\)の混合戦略\(\sigma _{i}^{\ast }\)が他のプレイヤーたちの混合戦略の組\(\sigma _{-i}^{\ast }\)に対する広義の最適反応になっていること、すなわち、\(G\)の混合拡張\(G^{\ast }\)において、\begin{equation*}\forall i\in I,\ \forall \sigma _{i}\in \Delta \left( S_{i}\right)
:F_{i}(\sigma _{i}^{\ast },\sigma _{-i}^{\ast })\geq F_{i}(\sigma
_{i},\sigma _{-i}^{\ast })
\end{equation*}が成立していることを意味します。
これまで何度か指摘したように、戦略型ゲーム\(G\)が有限ゲームである場合、その混合拡張\(G^{\ast }\)には必ず広義の混合戦略ナッシュ均衡が存在します。これはナッシュの定理(Nash’s theorem)と呼ばれる命題ですが、今回はこの命題の理論的な根拠を解説します。
有限な戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)には少なくとも1つの広義の混合戦略ナッシュ均衡が存在する。
ナッシュの定理の証明戦略
集合\(X\)のそれぞれの要素に対して集合\(Y\)の部分集合を1つずつ定める規則を\(X\)から\(Y\)への対応(correspondence)と呼び、これを、\begin{equation*}f:X\twoheadrightarrow Y
\end{equation*}で表します。また、\(X\)を\(f\)の始集合(initial set)と呼び、\(Y\)を\(f\)の終集合(final set)と呼びます。対応\(f\)が始集合\(X \)の要素\(x\)に対して定める\(Y\)の部分集合を\(f\left(x\right) \)で表し、これを\(f\)による\(x\)の像(image)と呼びます。
始集合と終集合がともに同じ集合\(X\)であるような対応\(f:X\twoheadrightarrow X\)に対して、\begin{equation*}x^{\ast }\in f\left( x^{\ast }\right)
\end{equation*}を満たすような点\(x^{\ast}\in X\)が存在する場合には、この点\(x^{\ast }\)を\(f\)の不動点(fixed point)と呼びます。
\begin{array}{cc}
\{1\} & if\ x<\frac{1}{2} \\
\left[ 0,1\right] & if\ x=\frac{1}{2} \\
\{0\} & if\ x>\frac{1}{2}\end{array}\right.
\end{equation*}と定義します。点\(\frac{1}{2}\in \left[ 0,1\right] \)に対して、\begin{equation*}\frac{1}{2}\in \left[ 0,1\right] =f\left( \frac{1}{2}\right)
\end{equation*}が成り立つため、\(\frac{1}{2}\)はこの対応\(f\)の不動点です。
対応は不動点を持つとは限りません。以下の例より明らかです。
\begin{array}{cc}
\{1\} & if\ x<\frac{1}{2} \\
\{0,1\} & if\ x=\frac{1}{2} \\
\{0\} & if\ x>\frac{1}{2}\end{array}\right.
\end{equation*}と定義します。\(f\)の定義より、任意の点\(x\in \left[0,1\right] \)に対して、\begin{equation*}x\not\in f\left( x\right)
\end{equation*}が成り立つため(確認してください)、この対応\(f\)には不動点が存在しません。
後ほど解説するように、集合\(X\)がユークリッド空間\(\mathbb{R} ^{n}\)の部分集合である場合、対応\(f:X\twoheadrightarrow X\)に不動点が存在するための条件が知られています。これを角谷の不動点定理(Kakutani’s fixedpoint theorem)と呼びます。混合戦略ナッシュ均衡を何らかの対応の不動点として表現した上で、その対応が角谷の不動点定理が要求する条件を満たすことを保証できれば、不動点定理により、混合戦略ナッシュ均衡が常に存在することを保証できます。以上がナッシュの定理の証明戦略です。そこで、まずは混合戦略ナッシュ均衡を対応の不動点として表現します。
不動点としての混合戦略ナッシュ均衡
戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)において、プレイヤー\(i\in I\)による広義の最適反応は他のプレイヤーたちの戦略の組\(\sigma _{-i}\in \Delta \left( S_{-i}\right) \)に依存して変化します。また、それぞれの\(\sigma _{-i}\)に対するプレイヤー\(i\)の広義の最適反応は1つであるとは限りません。以上を踏まえた上で、それぞれの\(\sigma _{-i}\in \Delta \left( S_{-i}\right) \)に対して、それに対するプレイヤー\(i\)の広義の最適反応から集合\begin{equation*}b_{i}(\sigma _{-i})=\{\sigma _{i}^{\ast }\in \Delta \left( S_{i}\right) \ |\
F_{i}(\sigma _{i}^{\ast },\sigma _{-i})=\max_{\sigma _{i}\in \Delta \left(
S_{i}\right) }F_{i}(\sigma _{i},\sigma _{-i})\}
\end{equation*}を像として定める対応\begin{equation*}
b_{i}:\Delta \left( S_{-i}\right) \twoheadrightarrow \Delta \left(
S_{i}\right)
\end{equation*}を定義し、これをプレイヤー\(i\)の広義の最適反応対応(weak best response correspondence)と呼びます。
プレイヤー\(i\)による広義の最適反応対応\(b_{i}\)が与えられたとき、プレイヤー\(i\)の混合戦略\(\sigma _{i}^{\ast }\)が他のプレイヤーたちの混合戦略の組\(\sigma _{-i}\)に対する広義の最適反応であることは、\begin{equation*}\sigma _{i}^{\ast }\in b_{i}\left( \sigma _{-i}\right)
\end{equation*}が成り立つこととして表現されます。したがって、混合戦略の組\(\sigma _{I}^{\ast }=\left( \sigma _{i}^{\ast }\right)_{i\in I}\)が広義の混合戦略ナッシュ均衡であることとは、\begin{equation*}\forall i\in I:\sigma _{i}^{\ast }\in b_{i}\left( \sigma _{-i}^{\ast }\right)
\end{equation*}が成り立つこととして表現されます。
\end{equation*}が成り立つことは、\(\sigma _{I}^{\ast }\)が\(G^{\ast }\)における広義の混合戦略ナッシュ均衡であるための必要十分条件である。
$$\begin{array}{ccc}
\hline
1\diagdown 2 & A & B \\ \hline A & -1,1 & 1,-1 \\ \hline B & 1,-1 & -1,1 \\ \hline\end{array}$$
プレイヤー\(i\ (=1,2)\)の混合戦略\(\sigma _{i}\)を、\begin{equation*}\left( \sigma _{i}\left( A\right) ,\sigma _{i}\left( B\right) \right)
=(\sigma _{i},1-\sigma _{i})
\end{equation*}と表記します。\(0\leq \sigma_{i}\leq 1\)です。プレイヤー\(2\)が混合戦略\(\sigma _{2}\)を選ぶとき、プレイヤー\(1\)が混合戦略\(\sigma _{1}\)から得る期待利得は、\begin{eqnarray*}F_{1}\left( \sigma _{1},\sigma _{2}\right) &=&-\sigma _{1}\sigma
_{2}+\sigma _{1}\left( 1-\sigma _{2}\right) +\left( 1-\sigma _{1}\right)
\sigma _{2}-\left( 1-\sigma _{1}\right) \left( 1-\sigma _{2}\right) \\
&=&-\left( 2\sigma _{1}-1\right) \left( 2\sigma _{2}-1\right)
\end{eqnarray*}であるため、プレイヤー\(1\)の広義の最適反応対応\(b_{1}:\Delta \left( S_{2}\right) \twoheadrightarrow\Delta \left( S_{1}\right) \)はそれぞれの\(\sigma _{2}\in \Delta \left( S_{2}\right) \)に対して、\begin{equation*}b_{1}\left( \sigma _{2}\right) =\left\{
\begin{array}{cc}
\left\{ 0\right\} & \left( if\ \sigma _{2}>\frac{1}{2}\right) \\
\left[ 0,1\right] & \left( if\ \sigma _{2}=\frac{1}{2}\right) \\
\left\{ 1\right\} & \left( if\ \sigma _{2}<\frac{1}{2}\right)
\end{array}\right.
\end{equation*}を定めます。プレイヤー\(1\)が混合戦略\(\sigma _{1}\)を選ぶとき、プレイヤー\(2\)が混合戦略\(\sigma _{2}\)から得る期待利得は、\begin{eqnarray*}F_{2}\left( \sigma _{1},\sigma _{2}\right) &=&\sigma _{1}\sigma _{2}-\sigma
_{1}\left( 1-\sigma _{2}\right) -\left( 1-\sigma _{1}\right) \sigma
_{2}+\left( 1-\sigma _{1}\right) \left( 1-\sigma _{2}\right) \\
&=&\left( 2\sigma _{1}-1\right) \left( 2\sigma _{2}-1\right)
\end{eqnarray*}であるため、プレイヤー\(2\)の広義の最適反応対応\(b_{2}:\Delta \left( S_{1}\right) \twoheadrightarrow\Delta \left( S_{2}\right) \)はそれぞれの\(\sigma _{1}\in \Delta \left( S_{1}\right) \)に対して、\begin{equation*}b_{2}\left( \sigma _{1}\right) =\left\{
\begin{array}{cc}
\left\{ 1\right\} & \left( if\ \sigma _{1}>\frac{1}{2}\right) \\
\left[ 0,1\right] & \left( if\ \sigma _{1}=\frac{1}{2}\right) \\
\left\{ 0\right\} & \left( if\ \sigma _{1}<\frac{1}{2}\right)
\end{array}\right.
\end{equation*}を定めます。このとき、\begin{eqnarray*}
\frac{1}{2} &\in &b_{1}\left( \frac{1}{2}\right) \\
\frac{1}{2} &\in &b_{2}\left( \frac{1}{2}\right)
\end{eqnarray*}が成り立つため、先の命題より\(\left( \sigma _{1},\sigma_{2}\right) =\left( \frac{1}{2},\frac{1}{2}\right) \)は広義の混合戦略ナッシュ均衡です。
プレイヤー集合が有限集合\begin{equation*}
I=\left\{ 1,\cdots ,n\right\}
\end{equation*}であるものとします。すべてのプレイヤーの広義の最適反応対応\(\left\{ b_{i}\right\} _{i\in I}\)が与えられれば、混合戦略からなるそれぞれの組\(\sigma _{I}\in \Delta \left( S_{I}\right) \)に対して、\begin{equation*}b_{I}\left( \sigma _{I}\right) =b_{1}\left( \sigma _{-1}\right) \times
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}を像として定める対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)を定義できます。
混合戦略の組\(\sigma _{I}^{\ast }\in\Delta \left( S_{I}\right) \)がこの対応\(b_{I}\)の不動点であるものとします。すなわち、\begin{equation*}\sigma _{I}^{\ast }\in b_{I}\left( \sigma _{I}^{\ast }\right)
\end{equation*}が成り立つということです。\(b_{I}\)の定義をもとに上の条件を詳しく書き直すと、\begin{equation*}\left( \sigma _{1}^{\ast },\cdots ,\sigma _{n}^{\ast }\right) \in
b_{1}\left( \sigma _{-1}^{\ast }\right) \times \cdots \times b_{n}\left(
\sigma _{-n}^{\ast }\right)
\end{equation*}すなわち、\begin{equation*}
\forall i\in I:\sigma _{i}^{\ast }\in b_{i}\left( \sigma _{-i}^{\ast }\right)
\end{equation*}となりますが、先の命題より、これは\(\sigma_{I}^{\ast }\)が広義の混合戦略ナッシュ均衡であることと必要十分です。
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}を像として定める対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)を定義する。このとき、混合戦略の組\(\sigma _{I}^{\ast }\in \Delta \left( S_{I}\right) \)に対して、\begin{equation*}\sigma _{I}^{\ast }\in b\left( \sigma _{I}^{\ast }\right)
\end{equation*}が成り立つこと、すなわち、点\(\sigma _{I}^{\ast }\)が対応\(b_{I}\)の不動点であることは、\(\sigma _{I}^{\ast }\)が\(G^{\ast }\)における広義の混合戦略ナッシュ均衡であるための必要十分条件である。
角谷の不動点定理
有限な戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)におけるすべてのプレイヤーの広義の最適反応対応から新たな対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)を定義した上で、広義の混合戦略ナッシュ均衡をこの対応\(b_{I}\)の不動点として表現することに成功しました。したがって、この対応\(b_{I}\)に不動点が存在することを保証できれば、\(G^{\ast }\)において広義の混合戦略ナッシュ均衡が常に存在することを保証できます。
対応に不動点が存在することを保証するためには、その対応はどのような条件を満たしていればよいのでしょうか。この問いに答えるのが以下の命題です。
\end{equation*}が成り立つ。
角谷の不動点定理が要求する条件を順番に解説します。1つ目の条件は、対応\(f:X\twoheadrightarrow X\)の始集合であるとともに終集合でもある\(X\)が、ユークリッド空間\(\mathbb{R} ^{n}\)の部分集合であるというものです。したがって、そこには位相が設定されています。
2つ目の条件は、集合\(X\)が空集合ではない(nonempty set)こと、すなわち、\begin{equation*}X\not=\phi
\end{equation*}が成り立つことです。\(X\)が空集合である場合、対応\(f:X\twoheadrightarrow X\)は不動点を持ちえません。
3つ目の条件は、集合\(X\)が\(\mathbb{R} ^{n}\)におけるコンパクト集合(compact set)であることです。\(\mathbb{R} ^{n}\)の部分集合がコンパクト集合であることは様々な形で表現可能ですが、\(X\)が\(\mathbb{R} ^{n}\)における有界な閉集合であることは\(X\)がコンパクト集合であるための必要十分条件です。もしくは、\(X\)の要素を項とする任意の点列が\(X\)の点に収束する部分列を持つこともまた\(X\)がコンパクト集合であるための必要十分条件です。より正確には、\begin{equation*}\forall n\in \mathbb{N} :x_{n}\in X
\end{equation*}を満たす点列\(\{x_{n}\}\)を任意に選んだときに、それに対して、\begin{equation*}\lim_{n\rightarrow \infty }x_{l\left( n\right) }\in X
\end{equation*}を満たす\(\{x_{n}\}\)の部分列\(\{x_{l\left( n\right) }\}\)が存在するということです。
4つ目の条件は、集合\(X\)が\(\mathbb{R} ^{n}\)における凸集合(convex set)であることです。ただし、集合\(X\)が凸集合であるとは、\(X\)に属する2つの点を任意に選んだとき、それらの点を結んで得られる線分上の任意の点もまた\(X\)の点であることを意味します。より正確には、\begin{equation*}\forall x,x^{\prime }\in X,\ \forall \lambda \in \left[ 0,1\right] :\lambda
x+\left( 1-\lambda \right) x^{\prime }\in X
\end{equation*}が成り立つということです。
5つ目の条件は、対応\(f:X\twoheadrightarrow X\)が非空値をとる(nonempty-valued)ことです。ただし、対応\(f\)が非空値をとるとは、\(X\)に属する任意の点\(x\)の\(f\)による像\(f\left( x\right) \)が非空集合であること、すなわち、\begin{equation*}\forall x\in X:f\left( x\right) \not=\phi
\end{equation*}が成り立つことを意味します。
6つ目の条件は、対応\(f:X\twoheadrightarrow X\)が閉値をとる(closed-valued)ことです。ただし、対応\(f\)が閉値をとるとは、\(X\)に属する任意の点\(x\)の\(f\)による像\(f\left( x\right) \)が閉集合であることを意味します。ただし、\(f\left( x\right) \)が閉集合であることとは、\(f\left( x\right) \)の要素を項とする任意の収束列の極限が\(f\left( x\right) \)の点であることを意味します。
7つ目の条件は、対応\(f:X\twoheadrightarrow X\)が凸値をとる(convex-valued)ことです。ただし、対応\(f\)が凸値をとるとは、\(X\)に属する任意の点\(x\)の\(f\)による像\(f\left( x\right) \)が凸集合であること、すなわち、\begin{equation*}\forall x\in X,\ \forall x^{\prime },x^{\prime \prime }\in f\left( x\right)
,\ \forall \lambda \in \left[ 0,1\right] :\lambda x^{\prime }+\left(
1-\lambda \right) x^{\prime \prime }\in f\left( x\right)
\end{equation*}が成り立つことを意味します。
8つ目の条件は、対応\(f:X\twoheadrightarrow X\)が上半連続(upper hemi-continy)であることです。これは、それぞれの点\(x\in X\)に対して\(f\left( x\right) \subset U\)を満たす\(X\)の開集合\(U\)を任意に選んだときに、それに対して、\begin{eqnarray*}&&\left( a\right) \ x\in V \\
&&\left( b\right) \ \forall v\in V:f\left( v\right) \subset U
\end{eqnarray*}を満たす\(X\)の開集合\(V\)が存在することを意味します。ただ、角谷の不動点定理は\(\mathbb{R} ^{n}\)の部分集合である\(X\)がコンパクト集合であることを要求しており、そのような場合には対応\(f:X\twoheadrightarrow X\)が上半連続であることを点列を用いて以下のように表現することも可能です。すなわち、\(\mathbb{R} ^{n}\)のコンパクト集合である\(X\)の要素を項とする収束点列\(\{x_{n}\},\{y_{n}\}\)の中でも、\begin{equation*}\forall n\in \mathbb{N} :y_{n}\in f\left( x_{n}\right)
\end{equation*}を満たすものを任意に選んだとき、これらの点列の極限の間に、\begin{equation*}
\lim_{n\rightarrow \infty }y_{n}\in f\left( \lim_{n\rightarrow \infty
}x_{n}\right)
\end{equation*}という関係が成り立つことは、\(f\)が上半連続であるための必要十分条件です。
\begin{array}{cc}
\{1\} & if\ x<\frac{1}{2} \\
\left[ 0,1\right] & if\ x=\frac{1}{2} \\
\{0\} & if\ x>\frac{1}{2}\end{array}\right.
\end{equation*}と定義します。集合\(\left[ 0,1\right] \)は\(1\)次元ユークリッド空間\(\mathbb{R} \)の部分集合であるとともに、非空かつコンパクトな凸集合であるため(確認してください)、不動点定理が要求する条件を満たしています。また、\(f\)は非空値かつ閉値かつ凸値をとる上半連続対応であるため(確認してください)、不動点定理が要求する条件を満たしています。したがって、不動点定理より、この対応\(f\)には不動点が存在することが保証されます。実際、\begin{equation*}\frac{1}{2}\in \left[ 0,1\right] =f\left( \frac{1}{2}\right)
\end{equation*}が成り立つため、\(\frac{1}{2}\)はこの対応\(f\)の不動点です。
\begin{array}{cc}
\{1\} & if\ x<\frac{1}{2} \\
\left\{ 0,1\right\} & if\ x=\frac{1}{2} \\
\{0\} & if\ x>\frac{1}{2}\end{array}\right.
\end{equation*}と定義します。集合\(\left[ 0,1\right] \)は不動点定理が要求する条件を満たしている一方、\(f\)は凸値をとらず、\(f\)は不動点定理が要求する条件を満たしていません。実際、\(f\)の定義より\(f\left( \frac{1}{2}\right) =\{0,1\}\)ですが、これに対して点\(0,1\in f\left( \frac{1}{2}\right) \)と\(\lambda =\frac{1}{2}\)を選ぶと、\begin{equation*}\lambda 0+\left( 1-\lambda \right) 1=\frac{1}{2}\cdot 0+\left( 1-\frac{1}{2}\right) 1=\frac{1}{2}
\end{equation*}となり、これは\(f\left( \frac{1}{2}\right) \)の要素ではないため\(f\)は凸値をとりません。したがって、この対応\(f\)の不動点の存在を不動点定理から保証することはできません。ちなみに、この対応\(f\)には不動点は存在しません。
ナッシュの定理
有限な戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)におけるすべてのプレイヤーの広義の最適反応対応から新たな対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)を定義した上で、広義の混合戦略ナッシュ均衡をこの対応\(b_{I}\)の不動点として表現しましたが、この対応\(b_{I}\)は不動点定理が要求する条件を満たすでしょうか。
対応\(b_{I}\)に対して不動点定理を適用するためには、まず、この対応の始集合であり終集合でもある以下の集合\begin{equation*}\Delta \left( S_{I}\right) =\Delta \left( S_{1}\right) \times \cdots \times
\Delta \left( S_{n}\right)
\end{equation*}がユークリッド空間\(\mathbb{R} ^{n}\)の部分集合であるとともに、非空かつコンパクトな凸集合である必要があります。ただ、一般に、非空集合どうしの直積は非空であり、コンパクト集合どうしの直積はコンパクトであり、凸集合どうしの直積は凸であるため、任意のプレイヤー\(i\)の混合戦略集合\(\Delta\left( S_{i}\right) \)が非空かつコンパクトな凸集合であることを示せば、上のように定義される\(\Delta \left( S_{I}\right) \)もまた非空かつコンパクトな凸集合であることを示したことになります。
\in \mathbb{R} ^{2}\ |\ \sigma _{i1}+\sigma _{i2}=1,\ \forall j\in \left\{ 1,2\right\}
:0\leq \sigma _{ij}\leq 1\right\}
\end{equation*}となります。ただし、\(\sigma _{ij}\)は混合戦略\(\sigma _{i}\)が\(j\)番目の純粋戦略\(s_{ij}\)に付与する確率です。この集合は下図において実線で描かれた線分として表現できます。ただし端点を含みます。つまり、この線分上にある点はそれぞれ異なる混合戦略に対応しています。図から明らかであるように、\(\Delta\left( S_{i}\right) \)は\(2\)次元ユークリッド空間\(\mathbb{R} ^{2}\)の部分集合であるとともに、非空かつコンパクトな凸集合です。ちなみに、このような\(\mathbb{R} ^{2}\)の部分集合を1次元の基本単体(standard \(1\) simplex)と呼びます。
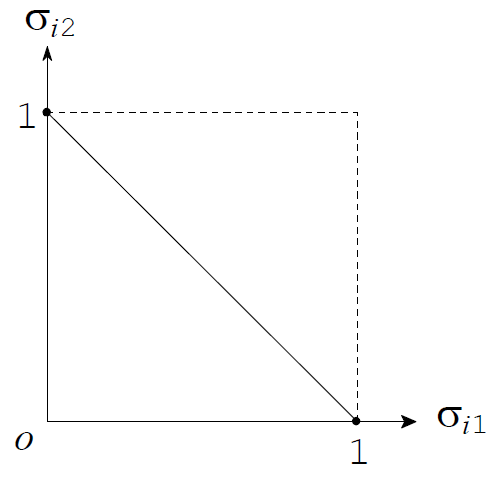
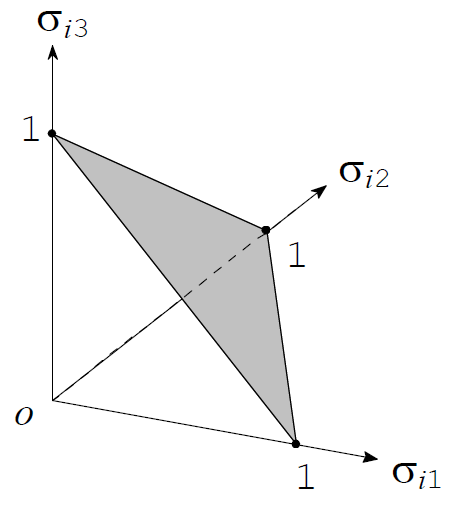
_{i3}\right) \in \mathbb{R} ^{3}\ \left\vert \ \sigma _{i1}+\sigma _{i2}+\sigma _{i3}=1,\ \forall j\in
\{1,2,3\}:0\leq \sigma _{ij}\leq 1\right. \right\}
\end{equation*}となりますが、これは下図においてグレーで描かれた領域として表現できます。ただし境界を含みます。つまり、この領域上にある点はそれぞれ異なる混合戦略に対応しています。図から明らかであるように、\(\Delta \left( S_{i}\right) \)は\(3\)次元ユークリッド空間\(\mathbb{R} ^{3}\)の部分集合であるとともに、非空かつコンパクトな凸集合です。ちなみに、このような\(\mathbb{R} ^{3}\)の部分集合を2次元の基本単体(standard \(2\)simplex)と呼びます。
問題としている戦略型ゲーム\(G\)は有限ゲームであるため、それぞれのプレイヤー\(i\)は有限個の純粋戦略を持ちます。その個数が\(m\)である場合、混合戦略集合は、\begin{equation*}\Delta \left( S_{i}\right) =\left\{ \left( \sigma _{i1},\cdots ,\sigma
_{im}\right) \in \mathbb{R} ^{m}\ \left\vert \ \sum\limits_{j=1}^{m}\sigma _{ij}=1\ ,\forall j\in
\{1,\cdots ,m\}:0\leq \sigma _{ij}\leq 1\right. \right\}
\end{equation*}と定義されます。\(m=1,2\)の場合については先に例で扱いましたが、一般に、この\(\Delta \left(S_{i}\right) \)は\(m\)次元ユークリッド空間\(\mathbb{R} ^{m}\)の部分集合であるとともに、非空かつコンパクトな凸集合になります。ちなみに、\(\mathbb{R} ^{m}\)におけるこのような部分集合を\(m-1\)次元の基本単体(standard \(m-1\) simplex)と呼びます。
\Delta \left( S_{n}\right)
\end{equation*}はユークリッド空間\(\mathbb{R} ^{mn}\)の部分集合であるとともに、非空かつコンパクトな凸集合である。
続いて、対応\(b_{I}\)が非空値をとることを示します。ただ、この対応\(b_{I}\)がそれぞれの\(\sigma _{I}\in \Delta \left( S_{I}\right) \)に対して定める像は、\begin{equation*}b_{I}\left( \sigma _{I}\right) =b_{1}\left( \sigma _{-1}\right) \times
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}であるため、それぞれのプレイヤー\(i\)の広義の最適反応対応\(b_{i}:\Delta \left( S_{-i}\right) \twoheadrightarrow \Delta \left(S_{i}\right) \)が非空値をとることを示せば、非空集合どうしの直積もまた非空であることにより、上のように定義される\(b_{I}\)もまた非空値をとることを示したことになります。
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}を像として定める対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)は非空値をとる。
続いて、対応\(b_{I}\)が閉値をとることを示します。ただ、この対応\(b_{I}\)がそれぞれの\(\sigma_{I}\in \Delta \left( S_{I}\right) \)に対して定める像は、\begin{equation*}b_{I}\left( \sigma _{I}\right) =b_{1}\left( \sigma _{-1}\right) \times
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}として定義されるため、それぞれのプレイヤー\(i\)の混合最適反応対応\(b_{i}:\Delta \left( S_{-i}\right)\twoheadrightarrow \Delta \left( S_{i}\right) \)が閉値をとることを示せば、閉集合どうしの直積もまた閉集合であることにより、上のように定義される\(b_{I}\)もまた閉値をとることを示したことになります。
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}を像として定める対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)は閉値をとる。
続いて、対応\(b_{I}\)が凸値をとることを示します。ただ、この対応\(b_{I}\)がそれぞれの\(\sigma_{I}\in \Delta \left( S_{I}\right) \)に対して定める像は、\begin{equation*}b_{I}\left( \sigma _{I}\right) =b_{1}\left( \sigma _{-1}\right) \times
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}として定義されるため、それぞれのプレイヤー\(i\)の混合最適反応対応\(b_{i}:\Delta \left( S_{-i}\right)\twoheadrightarrow \Delta \left( S_{i}\right) \)が凸値をとることを示せば、凸集合どうしの直積もまた凸集合であることにより、上のように定義される\(b_{I}\)もまた凸値をとることを示したことになります。
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}を像として定める対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)は凸値をとる。
最後に、対応\(b_{I}\)が上半連続であることを示します。先に示したように対応\(b_{I}\)の終集合\(\Delta \left( S_{I}\right) \)はコンパクト集合であるため、\(b_{I}\)が任意の点\(\sigma _{I}\in\Delta \left( S_{I}\right) \)において閉じていることを示せば目標は達成されます。そこで、\(b_{I}\)がある点\(\sigma _{I}\in \Delta \left( S_{I}\right) \)において閉じていないものと仮定して矛盾を導きます。
\cdots \times b_{n}\left( \sigma _{-n}\right)
\end{equation*}を像として定める対応\(b_{I}:\Delta \left( S_{I}\right) \twoheadrightarrow \Delta \left(S_{I}\right) \)を定義する。この対応\(b_{I}\)は上半連続性を満たす。
有限な戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)において、すべてのプレイヤーの広義の最適反応対応から新たな対応\(b_{I}\)を定義したとき、この対応は角谷の不動点定理が要求するすべての条件を満たすことが明らかになりました。したがって、この対応\(b_{I}\)には不動点が存在します。この対応\(b_{I}\)の不動点は\(G^{\ast }\)の広義の混合戦略ナッシュ均衡であることは先に指摘した通りです。したがって、有限ゲーム\(G\)の混合拡張\(G^{\ast }\)には広義の混合戦略ナッシュ均衡が必ず存在することが明らかになりました。
有限な戦略型ゲーム\(G\)の混合拡張\(G^{\ast }\)には少なくとも1つの広義の混合戦略ナッシュ均衡が存在する。
プレミアム会員専用コンテンツです
【ログイン】【会員登録】