レオンハルト・オイラーと「無限解析入門」
レオンハルト・オイラー(Leonhard Euler)は1707年4月15日にスイスのバーゼルで誕生しました。彼の父親は数々の有名な数学者を輩出したベルヌーイ家(Bernoulli)と親交があり、オイラー自身もヨハン・ベルヌーイ(Johann Bernoulli)の弟子として数学を学びます。

オイラーは1727年にヨハン・ベルヌーイの手配でロシア・サンクトペテルブルク科学アカデミーにポストを得ると、そこでダニエル・ベルヌーイ(Daniel Bernoulli)と共同研究を行います。後に彼は科学アカデミーの数学部門でトップの地位に就きます。しかし、ロシア皇帝エカチェリーナ1世の死によりサンクトペテルブルクが政情不安になると、オイラーは1741年にドイツへ移住し、ベルリン・アカデミーの会員になります。
ベルリン滞在中の1748 年、オイラーは『無限解析入門(Introduction to Analysis of the Infinite)』を出版します。オイラーの公式(Euler’s formula)とはその中で言及された、\begin{equation*}
e^{ix}=\cos x+i\sin x
\end{equation*}という等式です。さらに、オイラーの等式(Euler’s identity)はオイラーの公式の特殊ケースであり、\begin{equation*}
e^{i\pi }+1=0
\end{equation*}という等式です。これらの等式の意味や導出方法を後ほど解説します。

ノーベル物理学賞受賞者である米国の物理学者リチャード・ファインマン(Richard Phillips Feynman)によると、オイラーの等式は「我々の宝石(our jewel)」であり、「数学において最も優れた、驚異的と言ってよいほどの数式(one of the most remarkable, almost astounding, formulas in all of mathematics)」です。ファインマンに限らず、多くの数学者がオイラーの公式を絶賛し、その美しさを称えるのはなぜでしょうか。
ベルヌーイの思考実験
オイラーの公式やオイラーの等式の中に現れる、\begin{equation*}
e
\end{equation*}はオイラーの数(Euler’s number)として知られていますが、実はこれを発見したのはオイラーではなくヤコブ・ベルヌーイです。ベルヌーイがこの数を発見するきっかけとなったと言われる思考実験から話を始めましょう。
1年ごとに\(100\%\)の金利がつく場合に元本の\(x\)円を1年間単利で運用すると、1年後の元利合計は、\begin{equation*}x\left( 1+1\right) =2x\ \text{(円)}
\end{equation*}となります。つまり、1年間で元本はちょうど\(2\)倍になります。
金利を半分の\(50\%\)に下げる代わりに、1年間の半分である半年ごとに金利がつくものとしましょう。つまり、元本の\(x\)円を1年間複利で運用するということです。この場合、元本は半年ごとに\(1+\frac{1}{2}\)倍になるため、1年後の元利合計は、\begin{equation*}x\left( 1+\frac{1}{2}\right) ^{2}=2.25x\ \text{(円)}
\end{equation*}となります。つまり、1年間で元本は\(2.25\)倍になりますが、これは単利の場合の\(2\)倍よりも高い水準です。金利の水準と金利の発生期間をともに\(\frac{1}{2}\)にすると、複利の効果により元本の増加率が大きくなるというわけです。
さらに金利の水準と金利の発生期間を細かくしてみましょう。金利を\(\frac{1}{3}\)の\(\frac{100}{3}\%\)に下げる代わりに、1年間の\(\frac{1}{3}\)である4カ月ごとに金利がつくものとします。この場合、元本は4カ月ごとに\(1+\frac{1}{3}\)倍になるため、1年後の元利合計は、\begin{equation*}x\left( 1+\frac{1}{3}\right) ^{3}\approx 2.3704x\ \text{(円)}
\end{equation*}となります。つまり、1年間で元本は約\(2.3704\)倍になりますが、これは半年ごとの複利の場合の\(2.25\)倍よりも高い水準です。金利の水準と金利の発生期間を細かくすると、複利の効果により元本の増加率がさらに大きくなることが明らかになりました。
このような複利の効果は一般的に成り立つでしょうか。つまり、金利の水準と発生期間をさらに細かくしていった場合、1年間での元本の増加率はいくらでも大きくなり続けるのでしょうか。これが1683年にベルヌーイが提示した思考実験です。
オイラーの数
議論を一般化しましょう。金利の水準を\(100\%\)の\(\frac{1}{n}\)に相当する\(\frac{100}{n}\%\)に下げる代わりに、1年間の\(\frac{1}{n}\)に相当する\(\frac{1}{n}\)年ごとに金利がつくものとします。この場合、元本は\(\frac{1}{n}\)年ごとに\(1+\frac{1}{n}\)倍になるため、1年後の元利合計は、\begin{equation*}x\left( 1+\frac{1}{n}\right) ^{n}\ \text{(円)}
\end{equation*}となります。つまり、1年間で元本は\(\left( 1+\frac{1}{n}\right) ^{n}\)倍になります。
金利の水準と発生期間をどんどん細かくしていくと、1年間での元本の増加率はどのように変化していくでしょうか。つまり、\(n\)が増加するにつれて\(\left( 1+\frac{1}{n}\right) ^{n}\)の水準はどのように変化するでしょうか。複利の効果が一般的なものであるならば、\(n\)が増加するにつれて\(\left( 1+\frac{1}{n}\right) ^{n}\)もまたずっと増加し続けるはずです。
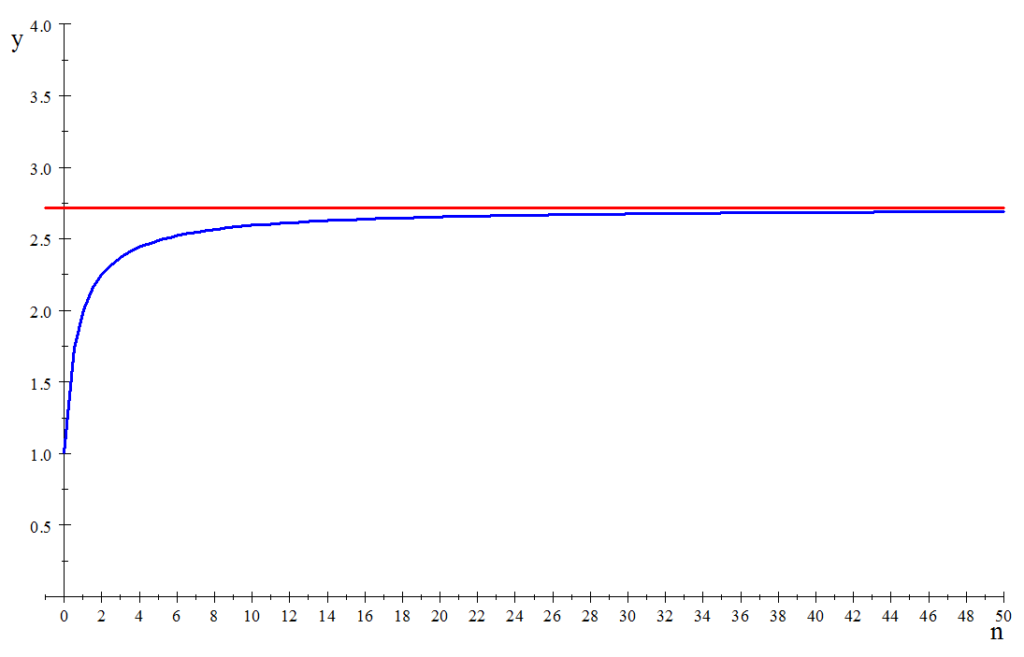
これを検証するために、\(n\)と\(\left( 1+\frac{1}{n}\right) ^{n}\)の関係を描いたのが上図中の青色のグラフです。横軸は\(n\)の水準を、縦軸は\(\left( 1+\frac{1}{n}\right) ^{n}\)の水準をそれぞれ表しています。グラフを観察すると、\(n\)が増加するにつれて\(\left( 1+\frac{1}{n}\right)^{n}\)も増加しますが、次第に、赤いグラフで表される値に限りなく近づいていく様子を確認できます。つまり、金利の水準と発生期間をどんどん細かくしていくと、1年間での元本の増加率は最初は増加しますが、いずれは一定の水準に落ち着きます。
なぜでしょうか。金利の発生期間を短くするほど複利の効果により元本はより速いスピードで増えていきますが、金利の水準を同時に下げているため、各期に得られる金利は小さくなっていきます。その結果、元本の増加率はなだらかになっていき、最終的には一定の水準に落ち着くのです。
\(n\)が大きくなるにつれて元本の増加率\(\left( 1+\frac{1}{n}\right) ^{n}\)は赤いグラフで表される値に限りなく近づいていきますが、この値がオイラーの数\(e\)に他なりません。この事実を定式化すると、\begin{equation*}\lim_{n\rightarrow \infty }\left( 1+\frac{1}{n}\right) ^{n}=e
\end{equation*}となります。金利の水準と発生期間をどんどん細かくしていくと、1年間での元本の増加率は最終的にある値に限りなく近づきますが、その値を\(e\)で表すということです。
この事実を発見したのはベルヌーイですが、オイラーがこの値\(e\)に自身の名前をつけたことから、今日において\(e\)はオイラーの数と呼ばれています。オイラーの数はネイピア数(Napier’s constant)や自然対数の底(base of natural logarithm)などと呼ばれることもあります。
無限級数としてのオイラーの数
オイラーの数\(e\)は、具体的には、\begin{equation*}e=2.7182818284\ …
\end{equation*}という無理数です。オイラーの数を導出する様々な方法が知られていますが、代表的なものは、\begin{equation}
e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\frac{1}{5!}+\frac{1}{6!}+\frac{1}{7!}+\cdots \quad \cdots (1)
\end{equation}という無限個の項の和(これを無限級数と呼びます)として表す手法です(テイラー展開と呼ばれる手法です)。ただし、\(n!\)は\(1\)から\(n\)までのすべての整数の積を表す記号(これを階乗と呼びます)であり、\begin{equation*}n!=1\cdot 2\cdot 3\cdot \cdots \cdot \left( n-1\right) \cdot n
\end{equation*}と定義されます。
さて、\(e=e^{1}\)であることを踏まえると、\(\left( 1\right) \)を、\begin{equation*}e^{1}=1+\frac{1}{1}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\frac{1}{5!}+\frac{1}{6!}+\frac{1}{7!}+\cdots
\end{equation*}と表現できます。ここで、\(e\)の指数を\(1\)から\(x\)へ一般化した\(e^{x}\)もまた無限級数で表せることが知られており、具体的には、
\begin{equation}
e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots \quad \cdots (2)
\end{equation}となります。つまり、\(\left( 2\right) \)において\(x=1\)とした特別な場合が\(\left(1\right) \)であり、逆に、\(\left(1\right) \)の一般化が\(\left( 2\right) \)です。
無限級数としての三角関数
話が脱線するようですが、三角関数\(\sin \left(x\right) \)および\(\cos \left( x\right) \)もまたそれぞれ無限級数で表されることが知られており、具体的には、\begin{eqnarray}\sin \left( x\right) &=&\frac{x}{1!}-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots \quad \cdots (3) \\
\cos \left( x\right) &=&1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots \quad \cdots (4)
\end{eqnarray}となります。これらに加えて、先の\(e^{x}\)に関する無限級数\begin{equation}e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots \quad \cdots (2)
\end{equation}も考察対象にしましょう。
オイラーの数と三角関数は互いに無関係の概念であるように思われます。しかし、三角関数に関する無限級数\(\left( 3\right) ,\left( 4\right) \)と、オイラーの数に関する無限級数\(\left( 2\right) \)は共通の項を持っているため、考えようによっては両者の間に何らかの関係を見出せそうです。この関係を具体的に示すのがオイラーの公式に他なりません。
オイラーの数と三角関数の関係を見出すため、三角関数に関する無限級数\(\left( 3\right) ,\left(4\right) \)を用いてオイラーの数に関する無限級数\(\left( 2\right) \)を再現できるか検討してみます。\begin{eqnarray}\sin \left( x\right) &=&\frac{x}{1!}-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots \quad \cdots (3) \\
\cos \left( x\right) &=&1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots \quad \cdots (4) \\
e^{x} &=&1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots \quad \cdots (2)
\end{eqnarray}試しに、\(\left( 3\right) \)と\(\left( 4\right) \)を足し合わせた上で項を並べ替えると,\begin{eqnarray*}&&\sin \left( x\right) +\cos \left( x\right) \\
&=&\left( \frac{x}{1!}-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots \right) +\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots \right) \quad \because \left( 3\right) ,\left( 4\right) \\
&=&1+\frac{x}{1!}-\frac{x^{2}}{2!}-\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}-\frac{x^{6}}{6!}-\frac{x^{7}}{7!}+\cdots
\end{eqnarray*}となります。この無限級数はオイラーの数に関する無限級数\(\left( 2\right) \)と似ていますが、この無限級数の項の中には負の記号で始まるものがあるため、2つの無限級数は完全には一致しません。両者を一致させるためには何らかの工夫が必要です。
虚数単位
オイラーの数に関する無限級数と、三角関数に関する無限級数を改めて見比べてみましょう。
\begin{eqnarray}
e^{x} &=&1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots \quad \cdots (2) \\
\sin \left( x\right) +\cos \left( x\right) &=&1+\frac{x}{1!}-\frac{x^{2}}{2!}-\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}-\frac{x^{6}}{6!}-\frac{x^{7}}{7!}+\cdots \quad \cdots (5)
\end{eqnarray}これらを一致させるためには、\(\left( 2\right) \)の中にある以下の項\begin{equation*}\frac{x^{2}}{2!},\ \frac{x^{3}}{3!},\ \frac{x^{6}}{6!},\ \frac{x^{7}}{7!},\cdots
\end{equation*}がいずれも負の記号で始まるように変換する必要があります。
ここで登場するのが虚数単位\(i\)です。任意の実数\(n\)の2乗\(n^{2}\)は\(0\)以上になるため、一般に、\begin{equation*}n^{2}=-1
\end{equation*}を満たす実数\(n\)は存在しません。そこで、上の等式を満たす(実数とは異なる)数を新たに定義した上で、それを虚数単位と呼び、記号\(i\)で表記します。つまり、虚数単位\(i\)とは、\begin{equation}i^{2}=-1 \quad \cdots (6)
\end{equation}を満たす数として定義されます。定義より、\begin{eqnarray*}
i^{2} &=&-1 \\
i^{3} &=&i\times i^{2}=i\times \left( -1\right) =-i \\
i^{4} &=&i^{2}\times i^{2}=\left( -1\right) \times \left( -1\right) =1 \\
i^{5} &=&i\times i^{2}\times i^{2}=i\times \left( -1\right) \times \left(
-1\right) =i \\
i^{6} &=&i^{2}\times i^{2}\times i^{2}=\left( -1\right) \times \left(
-1\right) \times \left( -1\right) =-1 \\
&&\cdots
\end{eqnarray*}などとなります。以下では、この虚数単位を用いてオイラーの数と三角関数を結びつけます。
オイラーの公式
これまでの議論を整理しましょう。まず、オイラーの数\(e\)に関しては、以下の関係\begin{equation}e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots \quad \cdots (2)
\end{equation}が成立します。また、三角関数に関しては、以下の関係\begin{eqnarray}
\sin \left( x\right) &=&\frac{x}{1!}-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots \quad \cdots (3) \\
\cos \left( x\right) &=&1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots \quad \cdots (4)
\end{eqnarray}が成り立ち、虚数単位\(i\)は、\begin{equation}i^{2}=-1 \quad \cdots (6)
\end{equation}を満たす数として定義されます。これらの概念を結び付けて1つの式で表します。まず、\(\left( 2\right) \)において\(e\)の指数を\(x\)から\(ix\)へ変更すると,\begin{equation*}e^{ix}=1+\frac{ix}{1!}+\frac{(ix)^{2}}{2!}+\frac{\left( ix\right) ^{3}}{3!}+\frac{\left( ix\right) ^{4}}{4!}+\frac{\left( ix\right) ^{5}}{5!}+\frac{\left( ix\right) ^{6}}{6!}+\frac{\left( ix\right) ^{7}}{7!}+\cdots
\end{equation*}を得ますが、虚数単位\(i\)の定義である\(\left( 6\right) \)を用いてこれを変形すると,\begin{eqnarray*}e^{ix} &=&1+\frac{ix}{1!}+\frac{i^{2}x^{2}}{2!}+\frac{i^{3}x^{3}}{3!}+\frac{i^{4}x^{4}}{4!}+\frac{i^{5}x^{5}}{5!}+\frac{i^{6}x^{6}}{6!}+\frac{i^{7}x^{7}}{7!}+\cdots \\
&=&1+\frac{ix}{1!}+\frac{\left( -1\right) x^{2}}{2!}+\frac{\left( -i\right)
x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{ix^{5}}{5!}+\frac{-x^{6}}{6!}+\frac{-ix^{7}}{7!}+\cdots \\
&=&1+\frac{ix}{1!}-\frac{x^{2}}{2!}-\frac{ix^{3}}{3!}+\frac{x^{4}}{4!}+\frac{ix^{5}}{5!}-\frac{x^{6}}{6!}-\frac{ix^{7}}{7!}+\cdots
\end{eqnarray*}となります。この無限級数の項を、虚数単位\(i\)を含むものとそうでないものに分けた上で並び替えると、\begin{eqnarray*}e^{ix} &=&\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots
\right) +\left( \frac{ix}{1!}-\frac{ix^{3}}{3!}+\frac{ix^{5}}{5!}-\frac{ix^{7}}{7!}+\cdots \right) \\
&=&\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots
\right) +i\left( \frac{x}{1!}-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots \right)
\end{eqnarray*}となりますが、左側の括弧の中身は\(\left( 4\right) \)と一致し、右側の括弧の中身は\(\left( 5\right) \)と一致します。したがって、\begin{equation*}e^{ix}=\cos \left( x\right) +i\sin \left( x\right)
\end{equation*}という関係が成り立つことが示されました。これがオイラーの公式です。
オイラーの公式の美しさは、互いに関係なさそうに思われる概念どうしの関係を1つの等式によって綺麗に表現している点にあります。つまり、オイラーの数\(e\)、三角関数\(\sin \left( x\right) \)および\(\cos\left( x\right) \)、そして虚数単位\(i\)という概念は互いに独立しているようでいて実は相互に関係しており、オイラーの公式はその関係を具体的に表現しています。
オイラーの等式
オイラーの等式はオイラーの公式の特殊ケースです。オイラーの公式\begin{equation*}
e^{ix}=\cos \left( x\right) +i\sin \left( x\right)
\end{equation*}において、\begin{equation*}
x=\pi
\end{equation*}とおくと、\begin{equation}
e^{i\pi }=\cos \left( \pi \right) +i\sin \left( \pi \right) \quad \cdots (7)
\end{equation}を得ます。\(\pi \)のサインとコサインは、\begin{eqnarray*}\sin \left( \pi \right) &=&0 \\
\cos \left( \pi \right) &=&-1
\end{eqnarray*}であるため、これらを使って\(\left( 7\right) \)を変形すると、\begin{equation*}e^{i\pi }=-1+0
\end{equation*}すなわち、\begin{equation*}
e^{i\pi }+1=0
\end{equation*}を得ます。これがオイラーの等式です。
オイラーの公式はオイラーの数、三角関数、虚数単位という3つの概念の関係を1本の等式で表しているのに対し、オイラーの等式はオイラーの数、円周率、虚数単位という3つの概念を1本の等式で表しています。

















