レーティング
対戦競技におけるプレイヤーの実力を表す指標をレーティング(rating)と呼びます。対戦競技には相手がいるため、プレイヤーの実力は絶対的なものではなく、他のプレイヤーとの比較の中で決まります。したがって、対戦競技におけるプレイヤーのレーティングは、他のプレイヤーとの対戦結果から決定するのがもっともらしいと言えます。強い相手に勝てば多くのスコアを獲得できるが、それほど強くない相手に勝ってもそれほどスコアを稼げない、そのような基準にもとづいてレーティングを決定するということです。
イロ・レーティングシステム(Elo rating system)とは、チェスや将棋など 1 対 1 の対戦競技において、対戦結果や対戦相手の強さを踏まえながらプレイヤーのレーティングを決める方法の 1 つです。イロ・レーティングはもともとチェスの実力を表すために考案されたものですが、現在では将棋や囲碁、アメフトやサッカー、テニスなどの様々な対戦競技において採用されています。
イロ・レーティングについて解説する前に、まずは私たちにとってなじみ深い勝率の概念について復習しましょう。
期待勝率とオッズ
あるプレイヤーが他のプレイヤーと対戦したときに勝利する確率を期待勝率(expected score)と呼びます。プレイヤー\(1\)がプレイヤー\(2\)と対戦したときの期待勝率を\(e_{12}\)で表すことにします。つまり、引き分けのない競技においてプレイヤー\(1,2\)が対戦したとき、プレイヤー\(1\)が\(75\%\)の確率で勝ち、\(25\%\)の確率で負けるならば、このことを、\begin{equation*}
e_{12}=0.75
\end{equation*}で表すということです。同じことをプレイヤー\(2\)の立場から考えると、\begin{equation*}
e_{21}=0.25
\end{equation*}となり、両者の間には、\begin{equation*}
e_{12}+e_{21}=1
\end{equation*}という関係が成り立ちます。
また、あるプレイヤーが他のプレイヤーと対戦した時に、自分の期待勝率が相手の期待勝率の何倍であるかを表す指標をオッズ(odds)と呼びます。上の例では、プレイヤー\(1\)が勝利するオッズは、\begin{equation*}
o_{12}=\frac{e_{12}}{e_{21}}=3
\end{equation*}となります。つまり、プレイヤー\(1\)の期待勝率はプレイヤー\(2\)の期待勝率の\(3\)倍であるとうことです。同じことをプレイヤー\(2\)の立場から考えると、\begin{equation*}
o_{21}=\frac{e_{21}}{e_{12}}=\frac{1}{3}
\end{equation*}となり、両者の間には、\begin{equation*}
o_{12}\times o_{21}=1
\end{equation*}という関係が成り立ちます。
引き分けが起こり得る競技の場合には、引き分けになる確率の半分をプレイヤーの期待勝率に加算することとします。つまり、引き分けは勝ちの半分とみなすということです。このルールのもとでは、プレイヤー\(1,2\)が対戦したときにプレイヤー\(1\)が\(50\%\)の確率で勝ち、\(20\%\)の確率で負け、\(30\%\)の確率で引き分けになることを、\begin{equation*}
e_{12}=0.5+\frac{0.3}{2}=0.65
\end{equation*}で表します。同じことをプレイヤー\(2\)の立場から考えると、\begin{equation*}
e_{21}=0.2+\frac{0.3}{2}=0.35
\end{equation*}となり、両者の間には、\begin{equation*}
e_{12}+e_{21}=1
\end{equation*}という関係が成り立ちます。この場合にもオッズを先ほどと同様に定義します。
期待確率とオッズに関する仮定
競技に参加するプレイヤーの中から 3 人を任意に選び、彼らをそれぞれ\(1,2,3\)と呼ぶこととします。プレイヤー\(1,2\)の間には、\begin{equation}
o_{12}=\frac{e_{12}}{e_{21}}=10 \quad\cdots (1)
\end{equation}という関係が成り立つものとします。つまり、プレイヤー\(1\)のプレイヤー\(2\)に対する期待勝率は、プレイヤー\(2\)のプレイヤー\(1\)に対する期待勝率の\(10\)倍であるということです。さらに、プレイヤー\(2,3\)の間には、\begin{equation}
o_{23}=\frac{e_{23}}{e_{32}}=10 \quad\cdots (2)
\end{equation}という関係が成り立つものとします。つまり、プレイヤー\(2\)のプレイヤー\(3\)に対する期待勝率は、プレイヤー\(3\)のプレイヤー\(2\)に対する期待勝率の\(10\)倍であるということです。
では、残された組み合わせであるプレイヤー\(1\)とプレイヤー\(3\)が対戦する場合にはどうなるでしょうか。\(\left( 1\right) \)と\(\left( 2\right) \)が与えられたとき、イロ・レーティングシステムにおいては、\begin{equation*}
o_{13}=o_{12}\times o_{23}=100
\end{equation*}という関係が成り立つものと仮定します(図 1)。
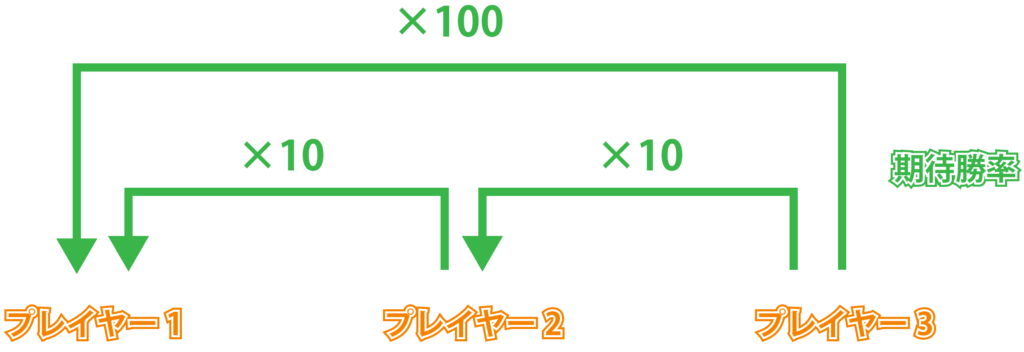
つまり、プレイヤー\(1,2,3\)について、\(1\)の\(2\)に対するオッズが\(10\)(\(1\)の\(2\)に対する勝率は\(2\)の\(1\)に対する勝率の\(10\)倍)で、\(2\)の\(3\)に対するオッズが\(10\)(\(2\)の\(3\)に対する勝率は\(3\)の\(2\)に対する勝率の\(10\)倍)であるとき、\(1\)の\(3\)に対するオッズを両者の積に相当する\(100\)(\(1\)の\(3\)に対する勝率は\(3\)の\(1\)に対する勝率の\(100\)倍)と定めるということです。現実にはプレイヤーの相性があるためこのような綺麗な関係は成立するとは限りませんが、イロ・レーティングシステムにおいては便宜的にこのような関係を仮定します。
期待勝率ないしオッズをレーティングに変換する
競技参加者の中から 2 人のプレイヤー\(i,j\)を任意に選んだとき、期待勝率\(e_{ij}\)やオッズ\(o_{ij}\)を通じて両者の実力関係を常に把握することができます。一方、レーティングの発想は、それぞれのプレイヤー\(i\)に固有の数値\(r_{i}\)を割り当てた上で、この数値の大小によってプレイヤー間の実力関係を把握する、というものです。
では、期待勝率やオッズからレーティングを導出するためにはどうすればよいでしょうか。イロ・レーティングシステムでは以下のルールを採用します。
o_{ij}=10\ \Leftrightarrow \ r_{i}-r_{j}=400
\end{equation*}という関係が成り立つものとする。
先ほどの例と同様に、プレイヤー\(1,2,3\)について、\begin{eqnarray}
o_{12} &=&\frac{e_{12}}{e_{21}}=10 \quad\cdots (1) \\
o_{23} &=&\frac{e_{23}}{e_{32}}=10 \quad\cdots (2)
\end{eqnarray}が成り立つものとします。このとき、イロ・レーティングの仮定より、\begin{equation}
o_{13}=o_{12}\times o_{23}=100=\left( 10^{2}\right) \quad\cdots (3)
\end{equation}が成り立つのでした。\(\left( 1\right) ,\left( 2\right) \)とレーティングの定義より、\begin{eqnarray*}
r_{1}-r_{2} &=&400 \\
r_{2}-r_{3} &=&400
\end{eqnarray*}が成り立つため、このとき、\begin{equation*}
r_{1}-r_{3}=800=\left( 400\times 2\right)
\end{equation*}となります。以上の関係を図解したものが図 2 です。
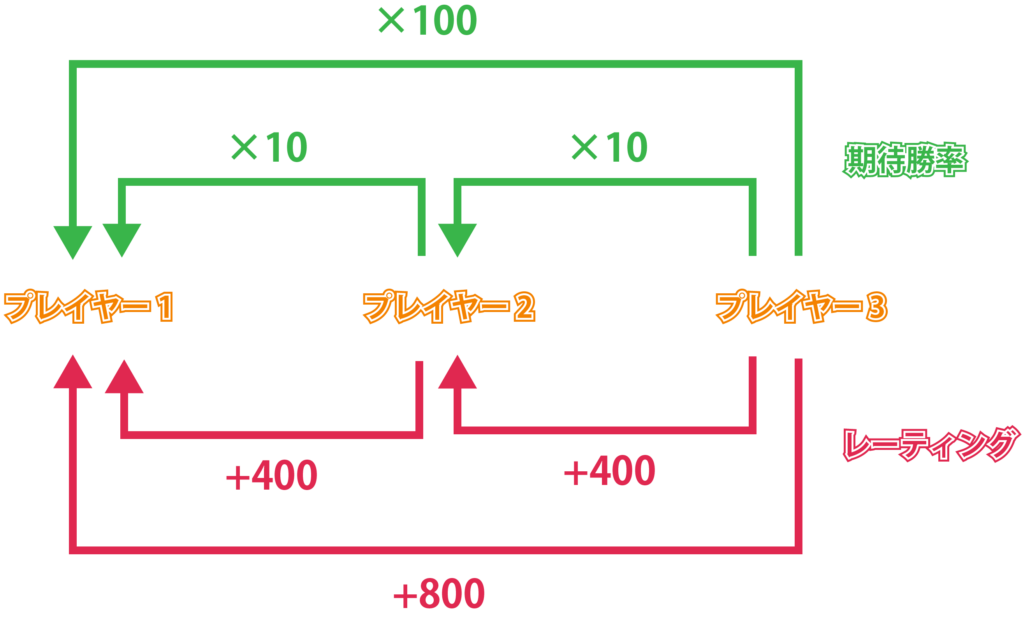
つまり、最も弱いプレイヤー\(3\)を基準として、彼よりも強いプレイヤー\(2\)を比べると、期待勝率は\(10\ \left( =10^{1}\right) \)倍になると同時にレーティングは\(400\ \left( =400\times 1\right) \)だけ加算されています。続いて、さらに強いプレイヤー\(1\)と比べると、期待勝率が\(100\ \left( =10^{2}\right) \)倍になると同時にレーティングは\(800\ \left( =400\times 2\right) \)だけ加算されています。
さらに強いプレイヤーについて同様に考えることで導かれる結論は、一般的に、期待勝率が\(10^{x}\)倍になるとレーティングは\(400x\)だけ加算されるということです。したがって、基準となるプレイヤーのレーティングを決めれば、あとは期待勝率もしくはオッズからすべてのプレイヤーのレーティングを導くことができます。
レーティングから期待勝率ないしオッズを予測する
前節では期待勝率もしくはオッズからレーティングを導出する方法を解説しましたが、逆に、レーティングから期待勝率もしくはオッズを予想することもできます。
繰り返しになりますが、一般に、期待勝率が\(10^{x}\)倍になるとレーティングは\(400x\)だけ加算されます。つまり、任意のプレイヤー\(i,j\)について、\(i\)の\(j\)に対する期待勝率\(e_{ij}\)が\(j\)の\(i\)に対する期待勝率\(e_{ji}\)の\(10^{x}\)倍であることは、\(i\)のレーティング\(r_{i}\)と\(j\)のレーティング\(r_{j}\)の差が\(400x\)であることと同義です。つまり、\begin{equation*}
\frac{e_{ij}}{e_{ji}}=10^{x}\ \Leftrightarrow \ r_{i}-r_{j}=400x
\end{equation*}という関係が成り立つということです。さらにここから、\begin{equation*}
\frac{e_{ij}}{e_{ji}}=10^{\frac{r_{i}-r_{j}}{400}}
\end{equation*}を得ます。これと、\begin{equation*}
e_{ij}+e_{ji}=1
\end{equation*}を踏まえると、\begin{equation*}
e_{ij}=\left( 1-e_{ij}\right) 10^{\frac{r_{i}-r_{j}}{400}}
\end{equation*}すなわち、\begin{equation*}
\left( 1+10^{\frac{r_{i}-r_{j}}{400}}\right) e_{ij}=10^{\frac{r_{i}-r_{j}}{400}}
\end{equation*}となります。したがって、\begin{eqnarray*}
e_{ij} &=&\frac{10^{\frac{r_{i}-r_{j}}{400}}}{1+10^{\frac{r_{i}-r_{j}}{400}}}
\\
&=&\frac{1}{10^{\frac{r_{j}-r_{i}}{400}}}\left/ \left( 1+\frac{1}{10^{\frac{r_{j}-r_{i}}{400}}}\right) \right. \\
&=&\frac{1}{10^{\frac{r_{j}-r_{i}}{400}}}\left/ \frac{1+10^{\frac{r_{j}-r_{i}}{400}}}{10^{\frac{r_{j}-r_{i}}{400}}}\right. \\
&=&\frac{1}{1+10^{\frac{r_{j}-r_{i}}{400}}}
\end{eqnarray*}を得ます。したがって、プレイヤー\(i,j\)のレーティング\(r_{i},r_{j}\)から上の関係を通じて期待勝率\(e_{ij}\)を予想することができます。
ちなみに、プレイヤー\(i,j\)のレーティングが等しい場合には、すなわち、\(r_{i}=r_{j}\)が成り立つ場合には、上の関係より、\begin{equation*}
e_{ij}=\frac{1}{1+1}=\frac{1}{2}
\end{equation*}となります。つまり、レーティングが等しいプレイヤーどうしが対戦すると勝率は五分五分になります。これはもっともらしい予測です。
レーティングの決定と更新
前節ではレーティングから期待勝率を予測する方法を解説しましたが、その際にプレイヤーのレーティングは与えられているという仮定のもとで話を進めました。では、そもそもレーティングをどのように求めればよいのでしょうか。対戦競技におけるレーティングは実際の対戦結果を反映する形で決定すべきですが、実際にプレイヤーたちが対戦を行う中で、レーティングをどのように決めていけばよいのでしょうか。
レーティングシステムを導入した直後にはデータがないため、それぞれのプレイヤー\(i\)のレーティング\(r_{i}\)を適当に決めることになります。さらにそこから、先に解説した方法により、任意の対戦相手\(j\)に対する期待勝率\(e_{ij}\)を求めることができます。今、実際にプレイヤー\(i,j\)が対戦したものとし、その結果を、\begin{equation*}
g_{ij}=\left\{
\begin{array}{cl}
1 & i\text{が勝った場合} \\
\frac{1}{2} & \text{引き分けの場合}
\\
0 & i\text{が負けた場合}\end{array}\right.
\end{equation*}で表します。その上で、対戦後のプレイヤー\(i\)のレーティング\(r_{i}^{\prime }\)を、\begin{equation*}
r_{i}^{\prime }=r_{i}+K\left( g_{ij}-e_{ij}\right)
\end{equation*}に更新します。ただし、\(K\)は定数です。つまり、プレイヤー\(i\)が勝った場合(\(g_{ij}=1\))にはプレイヤー\(i\)のレーティングを\(K\left( 1-e_{ij}\right) \)だけ増やし、負けた場合(\(g_{ij}=0\))には\(-Ke_{ij}\)だけ減らします。また、引き分けの場合(\(g_{ij}=\frac{1}{2}\))には\(K\left( \frac{1}{2}-e_{ij}\right) \)だけ変化させます。
プレイヤー\(i\)の期待勝率\(e_{ij}\)は相手プレイヤー\(j\)が強いほど小さくなるため、強い相手に勝てばレーティングは大きく増える一方で、強い相手に負けてもレーティングはそれほど減りません。逆に、弱い相手に勝ってもレーティングはそれほど増えませんが、弱い相手に負ければレーティングは大きく減少します。また、定数\(K\)の値が大きいほどレーティングの変動は大きくなり、逆に\(K\)の値が小さいほどレーティングの変動は小さくなります。

















