地球を囲む 2 本のロープの隙間
地球をゆがみのないきれいな球と仮定した上で、その赤道上にロープをたるまないように張って輪を作ります(図1の青い線)。ただし、ロープの太さは考えないものとします。
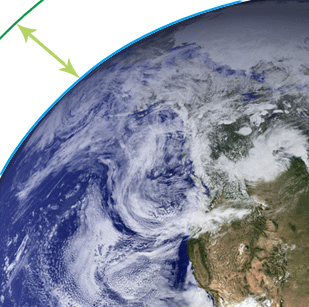
ロープの長さを 1 メートルだけ延長するとロープがたるみますが、このたるんだロープを使って先ほどの輪と同じ中心を持つ新たな輪を作ります(図 1 の濃い緑の線)。この 2 つの輪の間にはスペースができます(図 1 の黄緑の矢印)。
1 円玉を囲む 2 本の糸の隙間
先ほどと同様の作業を 1 円玉に対して行います。まず、1 円玉のまわりに糸をたるまないように張って輪を作ります(図2の青い線)。ただし、糸の太さは考えないものとします。
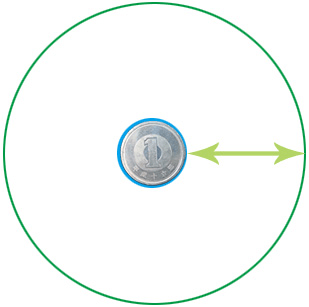
糸の長さを 1 メートルだけ延長すると糸がたるみますが、このたるんだ糸を使って先ほどの輪と同じ中心を持つ新たな輪を作ります(図2の濃い緑の線)。この 2 つの輪の間にはスペースができます(図 2 の黄緑の矢印)。
問題
地球を囲む 2 つの輪の円周の差と、1 円玉を囲む 2 つの輪の円周の差はともに 1 メートルです。では、先の 2 つの図にそれぞれ描かれた黄緑色の矢印の長さを比べたとき、どちらのほうが長いでしょうか?
地球と 1 円玉の大きさの違いを考慮すると、直感的には、1 円玉の場合の矢印のほうが地球の場合の矢印よりも長いと考えがちですが、実は、どちらの場合でも矢印の長さは同じです。以下ではそのことを証明しましょう。
証明
円周が\(C\)メートルで半径が\(r\)メートルの円があるとします(図 3 の青い円)。このとき、円周を\(1\)メートルだけ延長して\(C+1\)としたとき、新たな円の半径が\(R\)メートルになったとしましょう(図3の緑の円)。
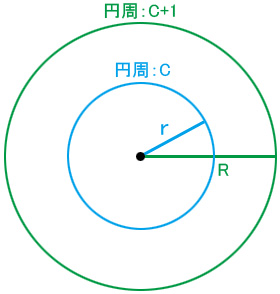
この 2 つの円について$$C=2 \pi r$$$$C+1=2 \pi R$$という関係が成り立ちますが、これらを変形すると、$$r=\frac{C}{2 \pi} \quad\cdots (1)$$$$R=\frac{C+1}{2 \pi} \quad\cdots (2)$$となります。
先の 2 つの例における黄緑の矢印の長さは,図 3 における\(R-r\)に相当しますが、\((1)\)と\((2)\)よりこれは、$$R-r=\frac{C+1}{2 \pi}-\frac{C}{2 \pi}=\frac{1}{2 \pi} \quad\cdots (3)$$となります。
注目すべきは、\((3)\)の値が定数であるということです。つまり,もとの円の大きさを規定する\(C\)の値とは関係なく、円周の長さを\(1\)メートルだけ伸ばした時にできる黄緑色の矢印の長さは、$$\frac{1}{2\pi} \approx 0.16$$という定数になります。たとえそれが地球でも、1円玉でも、結果は同じです。
ちなみに、この結果から逆に考えると、赤道の半径が約\(16\)センチ長くなったとき、新たな赤道をロープで囲うためには、ロープの長さを\(1\)メートルだけ伸ばせばよいことになります。
















