ジェナイル・ルーカスの定規
機械計算機が登場する前に日本ではそろばんが広く使われていましたが、西欧社会ではどのような道具が使われていたのでしょうか。フランス人の鉄道技術者ヘンリ・ルーカス(Henri Genaille)が 1891 年に開発したジェナイル・ルーカスの定規(Genaille-Lucas rulers)は、機械計算機が登場する以前の西欧社会において科学者や会計士の間で広く使われていた計算道具です。
それぞれの定規の上端には\(0\)から\(9\)までのいずれかの数字が書かれています。また、それぞれの定規の内部は 9 個の領域に分けられており、それぞれの領域の右側には数字が、左側には矢印が書かれています。

掛け算の方法
ジェナイル・ルーカスの定規を使って、例えば\(3271×4\)を計算する方法を解説します。
掛けられる数は\(3271\)ですので、上端に\(3,2,7,1\)とそれぞれ書かれた 4 本の定規を取り出してその順番通りに並べた上で、その左隣に\(0\)の定規を置きます。その様子を表したものが下図です。
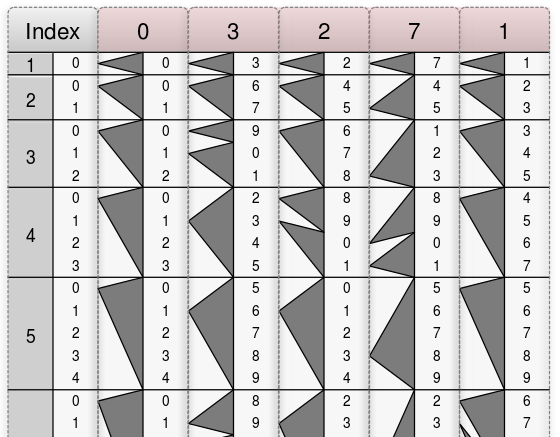
掛ける数は\(4\)ですので、上から 4 番目の行(Index が\(4\)の行)を見ます。下図で緑色に塗った行です。さらにその行の右隅かつ一番上の数字に注目します。下図で赤色に塗った場所の数字\(4\)です。
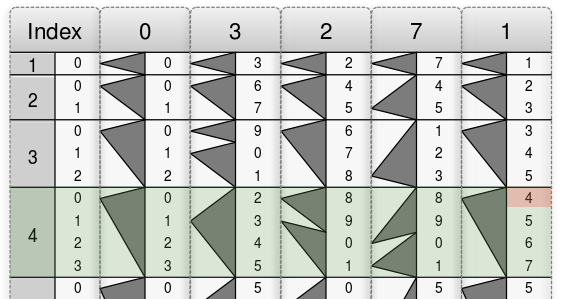
この数字\(4\)を確認したら、そこを出発点にして、左側の矢印に沿って左隣の定規へ移動すると\(8\)を得ます。以降も同様の手順によって左隣へ移動し続けると、最終的に、\(013084\)という数字を得ます。下図にその様子が描かれています。つまり、\(3271×4=13084\)です。
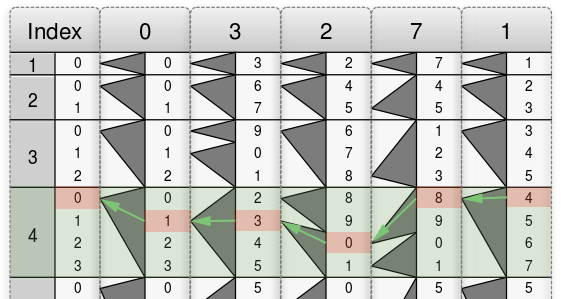
二桁以上の数どうしを掛ける方法
上の例では\(3271\times4\)を計算しましたが、そこでは掛ける数\(4\)に等しい Index の行に注目して答えを求めました。しかし、ジェナイル・ルーカスの定規には Index が\(1\)から\(9\)までしかないので、このままでは\(10\)以上の数を掛けることができません。二桁以上の数どうしを掛ける場合にはどうすればよいでしょうか。
例えば、ジェナイル・ルーカスの定規を使って\(3271\times45\)を計算する場合には、これを、
$$3271\times45=3271\times40+3271\times5$$と分割して考えます。\(3271\times4\)は定規を使って計算できるため、その答えを\(10\)倍すれば\(3271\times40\)の答えを得ます。さらに、\(3271\times 5\)も定規を使って計算します。こうして得られた 2 つの値を足せば\(3271\times45\)の解になります。
割り算の方法
ジェナイル・ルーカスの定規は掛け算を行うために開発されましたが、後に、割り算を行うための定規も開発されました。

割り算用の道具の使い方は先ほどと少しだけ違います。例として、\(6957÷6\)を計算する方法を解説します。
割られる数字は\(6957\)ですので、上端に\(6,9,5,7\)とそれぞれ書かれた 4 本の定規を取り出してその順番通りに並べた上で、その右隣に\(R\)の定規を置きます。その様子を表したものが下図です。ちなみに、\(R\)の定規は割り切れない場合の余りを特定するために使います。
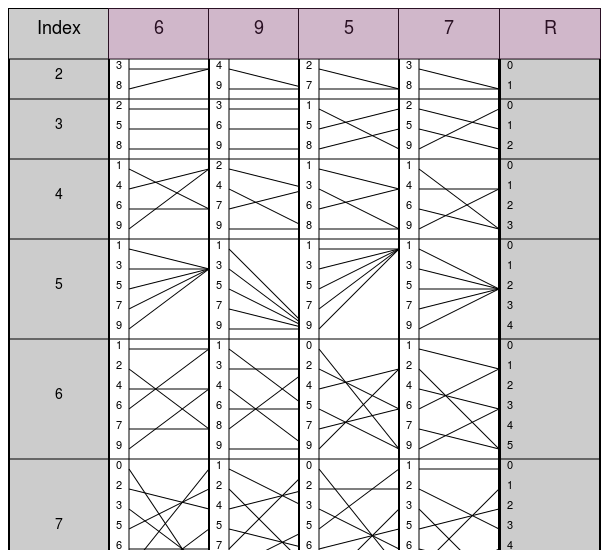
割る数は\(6\)ですので、上から 6 番目の行(Index が\(6\)の行)を見ます。下図で緑色に塗った行です。さらにその行の左隅かつ一番上の数字に注目します。下図で確認できるように、その数字は\(1\)です。
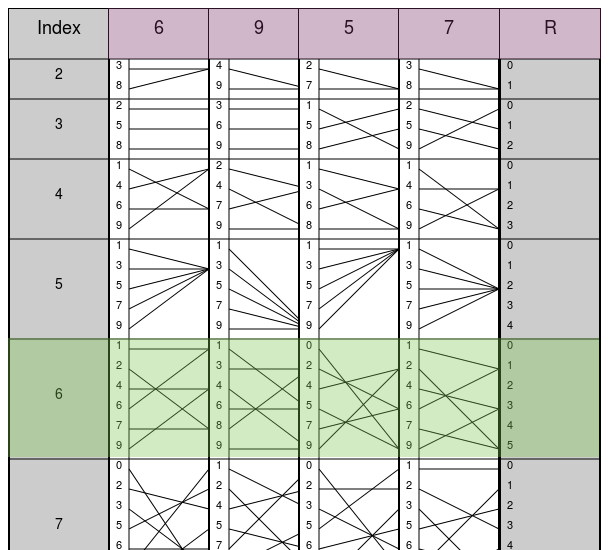
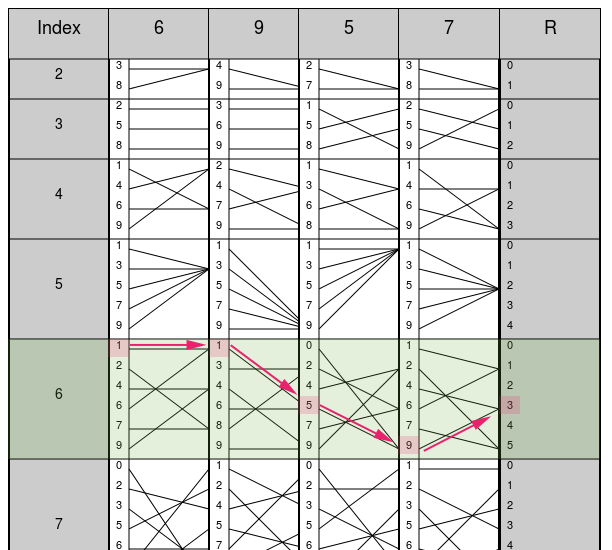
この数字\(1\)を確認したら、そこを出発点にして、右側の線に沿って右隣の定規へ移動すると\(1\)を得ます。以降も同様の手順によって右隣へ移動し続けると、最終的に、\(11593\)という数字を得ます。下図にその様子が描かれています。ただし、最後の\(3\)は\(R\) の定規の数字ですから、これは余りを表しています。つまり、\(6957÷6\)の解は\(1159\)余り\(3\)です。










プレミアム会員専用コンテンツです
【ログイン】【会員登録】