ブログ

ユダヤ教はキリスト教やイスラム教徒と同様、唯一絶対の神から与えられた啓典を信仰の基盤にする啓典宗教です。ユダヤ教の特徴は、集団救済の宗教であり、外的規範の実践を重視する規範宗教であるという点です。その意味を解説します。

写真が本格的に発達した19世紀の中頃は、絵画を中心に印象派が勃興した時代でもあります。印象派の作風は写実主義の対極にあるように見えますが、実は、その成り立ちは写真の発明や普及と深い関係があることが指摘されています。写真が普及するまでの歴史的経緯を追いながら、印象派に及ぼした影響について解説します。

0は自然数なのでしょうか。0を自然数に含める流儀と含めない流儀がありますが、どちらが正しいか決め手はありません。重要なのは定義を共有しておくことです。ここでは後続集合を用いた定義や、帰納的集合を用いた定義などを紹介します。

モノの値段は需要と供給がバランスする点に落ち着くのであるならば、商品の需要や供給が何らかの理由によって変化したとき、両者がバランスする点も変わるため、それに応じて商品の価格も変化することになります。では、商品の総需要や総供給はどのような理由から変化するのでしょうか。経済学に馴染みのない方向けに分かりやすく解説します。

モノやサービスの値段は需要と供給のバランスから決定されますが、その背後にあるメカニズムを経済学に馴染みのない方向けに分かりやすく解説します。

オークションの入札者は商品への評価額などを私的情報として持っています。入札者たちが自身の利益を最大化するために真の評価額とは異なる金額を入札する結果、オークション市場ではインセンティブの問題が発生します。オークション理論はインセンティブの問題を解消するためのオークションメカニズムを設計する学問です。

もともとメキシコ領であったカリフォルニアからテキサスへ至る領域は、テキサス併合やメキシコ・アメリカ戦争（米墨戦争）などを経てアメリカへ編入されます。こうした動きを正当化するスローガンとして叫ばれたのが「明白な使命（マニフェスト・デスティニー）」。その意味を、時代背景やアメリカという国の成り立ちとともに解説します。

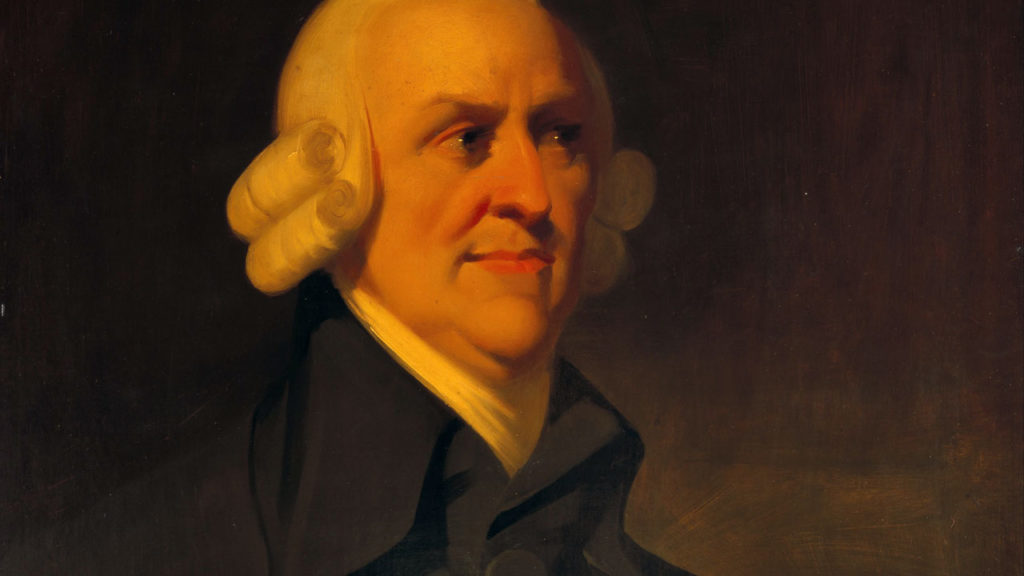
アダム・スミスの経済に関する思想は、社会秩序を導く人間本性について考察した著作である『道徳感情論』と関連付けながら理解する必要があります。今回はそのような立場からスミスの思想を概観します。

デカルトは『方法序説』において、理性の力を取り戻し、理性を活用するための方法を 4 つの準則としてまとめました。今回はデカルトの準則を参考にして、簡単には解けそうにない数学の問題に直面したときの対処方法を準則としてまとめます。

小学校などで割り算を学ぶ際に、「0では割ってはいけない」ことを理屈で説明するのではなく、守るべき「お約束」として習います。今回はその理由を体と呼ばれる数学概念を利用して解説します。

確率とは「何かの起こりやすさの度合いを数字で表現したもの」ですが、厳密に考えようとすると様々なアプローチがあります。今回は頻度による確率とラプラスの確率の2つの考え方について解説した上で、両者をつなぐ「ビュッフォンの針」という話をします。床に針を繰り返し落とすことで円周率を求めることができます。

対戦競技におけるプレイヤーの実力を表す指標をレーティングと呼びます。対戦競技には相手がいるため、レーティングは実際の対戦結果から決定すべきです。イロ・レーティングシステムは1対1の対戦競技におけるレーティング決定ルールであり、チェスや将棋、囲碁、アメフト、サッカー、テニスなどの様々な対戦競技において採用されています。

日本では計算機が登場する前にそろばんが広く使われていましたが、西欧社会ではどのような道具が使われていたのでしょうか。フランス人の鉄道技術者ヘンリ・ルーカスが 1891 年に開発したジェナイル・ルーカスの定規は、計算機が登場する以前の西欧社会において科学者や会計士の間で広く使われていた計算道具です。

金利とは何でしょうか？また、経済に大きな影響を与える金利は長期の実質金利ですが、それはなぜでしょうか？金利の水準はどのように決まるでしょうか？また、中央銀行である日銀が行う金利引き下げと量的緩和とはどのような政策であり、それはどのような効果を持つのでしょうか。以上のポイントについて分かりやすく解説します。

17 世紀にオランダで起きたチューチップ・バブルとはどのような現象でしょうか？また、その原因は？バブルを加速させた金融商品であるコール・オプションとは何か？また、資産価値を評価する考え方としてファンダメンタル価値理論と群集心理説の 2 つが有力ですが、これらの考え方を用いるとチューリップ・バブルはどのように解釈できるでしょうか？これらのポイントについて解説します。

オイラーの数、三角関数、虚数単位、円周率などの概念は互いに独立しているようで実は相互に関係しており、オイラーの等式はその関係をシンプルな 1 つの式で綺麗に表現しています。オイラーの等式の意味と、その導出方法を解説します。

TexMaker を使い日本語文書を作成するための環境を構築する方法について解説します。また、TexMaker のインターフェースを日本語化する方法も紹介します。

地球の赤道上にロープを張って輪を作ります。続いて、ロープの長さを1メートルだけ伸ばし、先の輪との同心円を作ります。この2つの同心円の半径の差を X と呼びます。続いて、1円玉の外周に糸を張って輪を作ります。続いて、糸の長さを1メートルだけ伸ばし、先の輪との同心円を作ります。この2つの同心円の半径の差を Y と呼びます。このとき、X=Y という関係が成り立ちます。