ユークリッド空間における集合間の距離

ユークリッド空間における集合間の距離

ユークリッド空間\(\left( \mathbb{R} ^{n},d\right) \)が与えられているものとします。ユークリッド距離関数\(d:\mathbb{R} ^{n}\times \mathbb{R} ^{n}\rightarrow \mathbb{R} \)は距離の公理に相当する以下の性質\begin{eqnarray*}&&\left( M_{1}\right) \ \forall \boldsymbol{x},\boldsymbol{y}\in \mathbb{R} ^{n}:d\left( \boldsymbol{x},\boldsymbol{y}\right) \geq 0 \\
&&\left( M_{2}\right) \ \forall \boldsymbol{x},\boldsymbol{y}\in \mathbb{R} ^{n}:\left[ d(\boldsymbol{x},\boldsymbol{y})=0\Leftrightarrow \boldsymbol{x}=\boldsymbol{y}\right] \\
&&\left( M_{3}\right) \ \forall \boldsymbol{x},\boldsymbol{y}\in \mathbb{R} ^{n}:d\left( \boldsymbol{x},\boldsymbol{y}\right) =d\left( \boldsymbol{y},\boldsymbol{x}\right) \\
&&\left( M_{4}\right) \ \forall \boldsymbol{x},\boldsymbol{y},\boldsymbol{z}\in \mathbb{R} ^{n}:d\left( \boldsymbol{x},\boldsymbol{z}\right) \leq d\left( \boldsymbol{x},\boldsymbol{y}\right) +d\left( \boldsymbol{y},\boldsymbol{z}\right)
\end{eqnarray*}を満たします。ユークリッド距離関数\(d\)はユークリッド空間\(\mathbb{R} ^{n}\)に属する2つの点\(\boldsymbol{x},\boldsymbol{y}\)の間の距離\(d\left( \boldsymbol{x},\boldsymbol{y}\right) \)を定めますが、距離関数\(d\)を活用することにより\(\mathbb{R} ^{n}\)の部分集合どうしの距離を定義することができます。

\(\mathbb{R} ^{n}\)の空ではない部分集合\(A,B\)を任意に選びます。この2つの集合の距離としては、\(A\)に属する点と\(B\)に属する点の間の距離の中でも最も短いものを採用します。つまり、\(A\)の点\(\boldsymbol{a}\)と\(B\)の点\(\boldsymbol{b}\)をそれぞれ任意に選んだとき、この2つの点の間の距離は\(d\left( \boldsymbol{a},\boldsymbol{b}\right) \)となるため、この距離がとり得る値の範囲は、\begin{equation}\left\{ d\left( \boldsymbol{a},\boldsymbol{b}\right) \in \mathbb{R} \ |\ \boldsymbol{a}\in A\wedge \boldsymbol{b}\in B\right\} \quad \cdots (1)
\end{equation}となりますが、この集合に属する値の中で最も小さいものとして、\(A\)と\(B\)の間の距離を定義するということです。

一般に、\(\mathbb{R} \)の非空な部分集合に対してその最小値は存在するとは限らないため、\(\mathbb{R} \)の部分集合である\(\left(1\right) \)についても、その最小値は存在するとは限りません。したがって、\(A\)と\(B\)の間の距離を\(\left( 1\right) \)の最小値と定義してしまうと、集合の間の距離が定まらないという事態が起こり得ます。このような事態を回避するために、\(A\)と\(B\)の間の距離を\(\left( 1\right) \)の最小値として定義するのではなく、\(\left( 1\right) \)の下限として定義した上で、これを、\begin{equation*}d\left( A,B\right) =\inf \left\{ d\left( \boldsymbol{a},\boldsymbol{b}\right) \in \mathbb{R} \ |\ \boldsymbol{a}\in A\wedge \boldsymbol{b}\in B\right\}
\end{equation*}で表記します。これを\(A\)から\(B\)へのユークリッド距離（Euclidean distance from \(A\) to \(B\)）と呼びます。

\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)に対して、その要素である\(\boldsymbol{a}\in A\)と\(\boldsymbol{b}\in B\)をそれぞれ任意に選びます。距離関数\(d\)の非負性よりそれらの間の距離\(d\left( \boldsymbol{a},\boldsymbol{b}\right) \)は非負の実数になります。したがって、先の集合\begin{equation*}\left\{ d\left( \boldsymbol{a},\boldsymbol{b}\right) \in \mathbb{R} \ |\ \boldsymbol{a}\in A\wedge \boldsymbol{b}\in B\right\}
\end{equation*}は非負の実数からなる\(\mathbb{R} \)の部分集合であるため下に有界です。すると、\(\mathbb{R} \)の連続性（下限性質）より、その下限\begin{equation*}\inf \left\{ d\left( \boldsymbol{a},\boldsymbol{b}\right) \in \mathbb{R} \ |\ \boldsymbol{a}\in A\wedge \boldsymbol{b}\in B\right\}
\end{equation*}すなわち\(d\left( A,B\right) \)が存在することが保証されます。しかも、\(\mathbb{R} \)の非空な部分集合の下限が存在する場合、それは必ず1つの実数として定まるため、\(d\left( A,B\right) \)もまた常に1つの実数として定まることが保証されます。以上の理由により、\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)をそれぞれ任意に選ぶと、\(A\)から\(B\)への距離\(d\left( A,B\right) \)は常に存在し、それは1つの有限な実数として定まることが保証されます。このような事情を踏まえると、それぞれの順序対\(\left( A,B\right) \in \mathcal{P}\left( \mathbb{R} ^{n}\right) \backslash \left\{ \phi \right\} \times \mathcal{P}\left( \mathbb{R} ^{n}\right) \backslash \left\{ \phi \right\} \)に対して、\(A\)から\(B\)への距離\(d\left( A,B\right) \in \mathbb{R} \)を定める実数値関数\begin{equation*}d:\mathcal{P}\left( \mathbb{R} ^{n}\right) \backslash \left\{ \phi \right\} \times \mathcal{P}\left( \mathbb{R} ^{n}\right) \backslash \left\{ \phi \right\} \rightarrow \mathbb{R} \end{equation*}が定義可能です。ただし、\(\mathcal{P}\left( \mathbb{R} ^{n}\right) \)は\(\mathbb{R} ^{n}\)のべき集合です。

\(\mathbb{R} ^{n}\)の非空な部分集合\(A\)を任意に選んだとき、空集合\(\phi \)との距離に関しては、便宜上、\begin{equation*}d\left( A,\phi \right) =d\left( \phi ,A\right) =d\left( \phi ,\phi \right)
=+\infty
\end{equation*}と定めます。

例（集合の間の距離）

\(2\)次元ユークリッド空間\(\mathbb{R} ^{2}\)における距離関数\(d:\mathbb{R} ^{2}\times \mathbb{R} ^{2}\rightarrow \mathbb{R} \)はそれぞれの\(\left( \boldsymbol{x},\boldsymbol{y}\right) \in \mathbb{R} ^{2}\times \mathbb{R} ^{2}\)に対して、\begin{equation*}d\left( \boldsymbol{x},\boldsymbol{y}\right) =\sqrt{\left(
x_{1}-y_{1}\right) ^{2}+\left( x_{2}-y_{2}\right) ^{2}}
\end{equation*}を定めます。\(\mathbb{R} ^{2}\)の非空な部分集合である以下の2つの集合\begin{eqnarray*}A &=&\{\left( x,y\right) \in \mathbb{R} ^{2}\ |\ x^{2}+y^{2}\leq 1\} \\
B &=&\{\left( x,y\right) \in \mathbb{R} ^{2}\ |\ 2\leq x\leq 4,\ 2\leq y\leq 4\}
\end{eqnarray*}に注目します。下図中の円盤が\(A\)に、正方形が\(B\)にそれぞれ対応します。

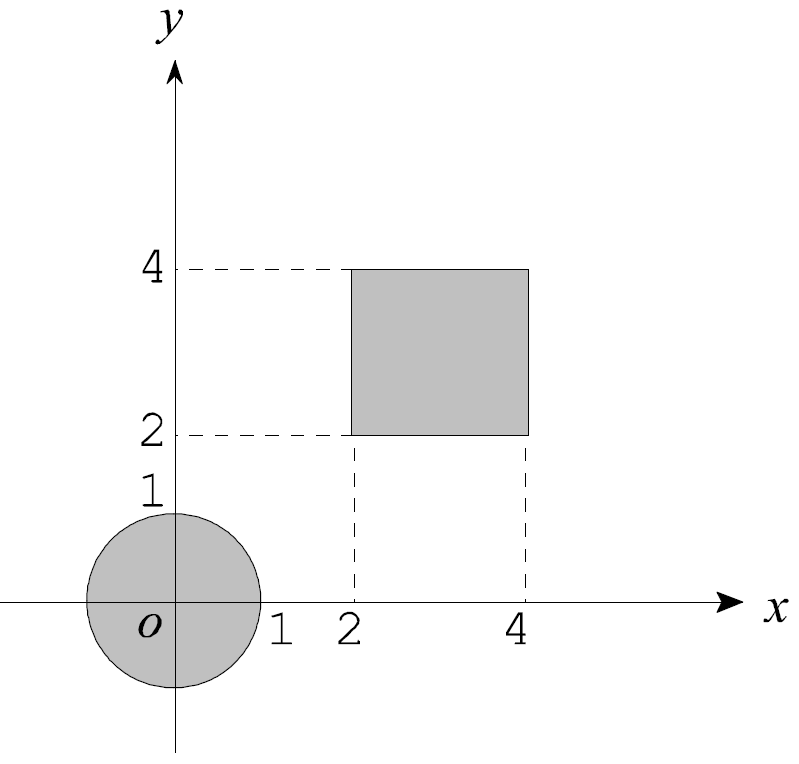
\(A\)と\(B\)の間の距離は\(A\)上の点\(\boldsymbol{a}=\left( \frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right) \)と\(B\)上の点\(\boldsymbol{b}=\left(2,2\right) \)の間の距離\begin{eqnarray*}d\left( A,B\right) &=&d\left( \boldsymbol{a},\boldsymbol{b}\right) \\
&=&\sqrt{\left( 2-\frac{\sqrt{2}}{2}\right) ^{2}+\left( 2-\frac{\sqrt{2}}{2}\right) ^{2}} \\
&=&2\sqrt{2}-1
\end{eqnarray*}となります。

ユークリッド空間における点と集合の距離

ユークリッド空間\(\mathbb{R} ^{n}\)の空ではない部分集合\(A,B\)の間の距離を、\begin{equation*}d\left( A,B\right) =\inf \left\{ d\left( \boldsymbol{a},\boldsymbol{b}\right) \in \mathbb{R} \ |\ \boldsymbol{a}\in A\wedge \boldsymbol{b}\in B\right\}
\end{equation*}と定義しました。以上を踏まえた上で、\(\mathbb{R} ^{n}\)の点\(\boldsymbol{x}\)から非空な部分集合\(A\)の間の距離としては、1点集合\(\left\{ \boldsymbol{x}\right\} \)と集合\(A\)の間の距離\(d\left( \left\{ \boldsymbol{x}\right\} ,A\right) \)を採用し、これを、\begin{eqnarray*}d\left( \boldsymbol{x},A\right) &=&d\left( \left\{ \boldsymbol{x}\right\}
,A\right) \\
&=&\inf \left\{ d\left( \boldsymbol{x},\boldsymbol{a}\right) \in \mathbb{R} \ |\ \boldsymbol{a}\in A\right\}
\end{eqnarray*}で表記します。

\(\mathbb{R} ^{n}\)の点\(\boldsymbol{x}\)を任意に選んだとき、空集合\(\phi \)との距離に関しては、便宜上、\begin{equation*}d\left( \boldsymbol{x},\phi \right) =+\infty
\end{equation*}と定めます。

例（点と集合の距離）

\(2\)次元ユークリッド空間\(\mathbb{R} ^{2}\)における距離関数\(d:\mathbb{R} ^{2}\times \mathbb{R} ^{2}\rightarrow \mathbb{R} \)はそれぞれの\(\left( \boldsymbol{x},\boldsymbol{y}\right) \in \mathbb{R} ^{2}\times \mathbb{R} ^{2}\)に対して、\begin{equation*}d\left( \boldsymbol{x},\boldsymbol{y}\right) =\sqrt{\left(
x_{1}-y_{1}\right) ^{2}+\left( x_{2}-y_{2}\right) ^{2}}
\end{equation*}を定めます。\(\mathbb{R} ^{2}\)の非空な部分集合である以下の集合\begin{equation*}A=\{\left( x,y\right) \in \mathbb{R} ^{2}\ |\ 2\leq x\leq 4\wedge 2\leq y\leq 4\}
\end{equation*}に注目します。下図中の正方形が\(A\)に対応します。

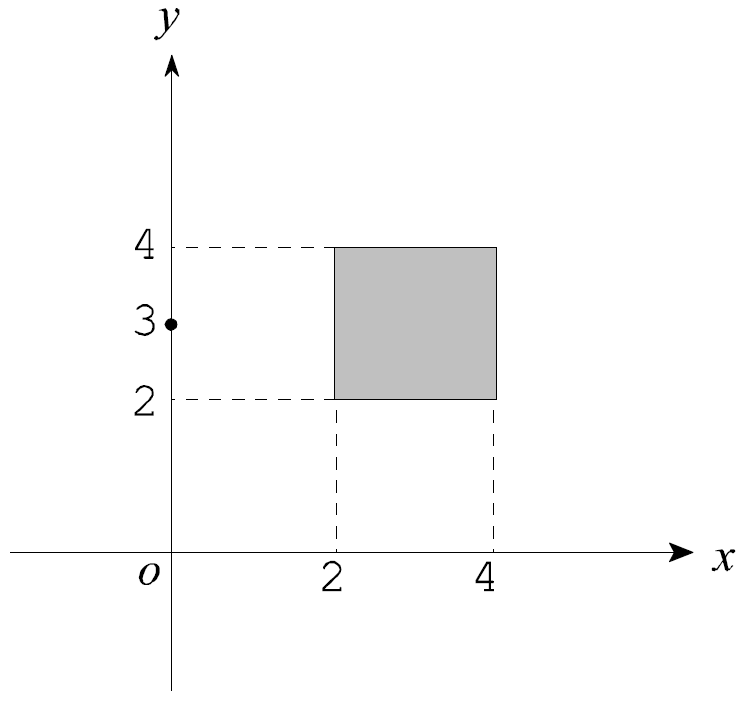
点\(\left( 0,3\right) \)と集合\(A\)の距離は、点\(\left( 0,3\right) \)と\(A\)上の点\(\left( 2,3\right) \)の間の距離と一致するため、\begin{eqnarray*}d\left( \left( 0,3\right) ,A\right) &=&d\left( \left( 0,3\right) ,\left(
2,3\right) \right) \\
&=&\sqrt{\left( 0-2\right) ^{2}+\left( 3-3\right) ^{2}} \\
&=&2
\end{eqnarray*}となります。

集合間の距離と非負性

ユークリッド空間\(\mathbb{R} ^{n}\)の部分集合どうしのユークリッド距離\begin{equation*}d:\mathcal{P}\left( \mathbb{R} ^{n}\right) \backslash \left\{ \phi \right\} \times \mathcal{P}\left( \mathbb{R} ^{n}\right) \backslash \left\{ \phi \right\} \rightarrow \mathbb{R} \end{equation*}もまた距離の公理を満たすのでしょうか。なお、\(\mathcal{P}\left( \mathbb{R} ^{n}\right) \)は\(\mathbb{R} ^{n}\)のべき集合を表す記号です。

\(\mathbb{R} ^{n}\)の部分集合どうしの距離は非負性を満たします。つまり、\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)を任意に選んだとき、\begin{equation*}d\left( A,B\right) \geq 0
\end{equation*}が成り立ちます。\(A\)から\(B\)への距離は必ず非負の実数になるということです。特に、\(A\)と\(B\)が交わる場合、\(A\)から\(B\)への距離は\(0\)になります。

点と集合の距離は集合間の距離の特殊ケースであるため、上の命題より以下を得ます。

集合間の距離と不可識別者同一性

ユークリッド空間\(\mathbb{R} ^{n}\)の部分集合どうしの距離は不可識別者同一性を満たすとは限りません。つまり、\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)に対して、\begin{equation*}d\left( A,B\right) =0\Leftrightarrow A=B
\end{equation*}は成り立つとは限りません。以下の例より明らかです。

集合間の距離と対称性

ユークリッド空間\(\mathbb{R} ^{n}\)の部分集合どうしの距離は対称性を満たします。つまり、\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)を任意に選んだとき、\begin{equation*}d\left( A,B\right) =d\left( B,A\right)
\end{equation*}が成り立ちます。\(A\)から\(B\)への距離と\(B\)から\(A\)への距離は等しいことが保証されるということです。このような事情を踏まえると、\(A\)から\(B\)への距離を\(A\)と\(B\)の間の距離（distance between \(A\) and \(B\)）と言っても差し支えありません。

点と集合の距離は集合間の距離の特殊ケースであるため、上の命題より以下を得ます。

集合間の距離と三角不等式

ユークリッド空間\(\mathbb{R} ^{n}\)の部分集合どうしの距離は三角不等式を満たすとは限りません。つまり、\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B,C\)に対して、\begin{equation*}d\left( A,C\right) \leq d\left( A,B\right) +d\left( B,C\right)
\end{equation*}は成り立つとは限りません。以下の例より明らかです。

一方、以下の関係は成立します。

以下の関係も成立します。

ミンコフスキー差と集合の間の距離

ユークリッド空間\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)を任意に選んだとき、\begin{equation*}A-B=\left\{ \boldsymbol{a}-\boldsymbol{b}\in \mathbb{R} ^{n}\ |\ \boldsymbol{a}\in A\wedge \boldsymbol{b}\in B\right\}
\end{equation*}と定義される\(\mathbb{R} ^{n}\)の部分集合\(A\)と\(B\)のミンコフスキー差（Minkowski difference）と呼びます。つまり、\(A\)の点と\(B\)の点のベクトル差からなる集合が\(A-B\)です。ミンコフスキー差は差集合\begin{equation*}A\backslash B=\left\{ \boldsymbol{x}\in \mathbb{R} ^{n}\ |\ \boldsymbol{x}\in A\wedge \boldsymbol{x}\not\in B\right\}
\end{equation*}とは異なる概念であることに注意してください。

\(\mathbb{R} ^{n}\)の非空な部分集合\(A,B\)が与えられたとき、\begin{equation*}d\left( A,B\right) =d\left( \left\{ \boldsymbol{0}\right\} ,A-B\right)
\end{equation*}という関係が成り立ちます。つまり、集合\(A,B\)の間の距離は、点\(\boldsymbol{0}\)とミンコフスキー差\(A-B\)の間の距離と一致します。

演習問題